Scalable spin squeezing from finite-temperature easy-plane magnetism

Abstract

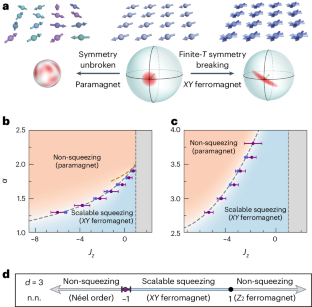
Spin squeezing is a form of entanglement that reshapes the quantum projection noise to improve measurement precision. Here, we provide numerical and analytic evidence for the following conjecture: any Hamiltonian exhibiting finite-temperature easy-plane ferromagnetism can be used to generate scalable spin squeezing, thereby enabling quantum-enhanced sensing. Our conjecture is guided by a connection between the quantum Fisher information of pure states and the spontaneous breaking of a continuous symmetry. We demonstrate that spin squeezing exhibits a phase diagram with a sharp transition between scalable squeezing and non-squeezing. This transition coincides with the equilibrium phase boundary for XY order at a finite temperature. In the scalable squeezing phase, we predict a sensitivity scaling that lies between the standard quantum limit and the scaling achieved in all-to-all coupled one-axis twisting models. A corollary of our conjecture is that short-ranged versions of two-axis twisting cannot yield scalable metrological gain. Our results provide insights into the landscape of Hamiltonians that can be used to generate metrologically useful quantum states. Generating highly squeezed states for quantum sensing requires precise entanglement properties, which makes it a hard task. Now a conjecture identifies a realistic regime of magnetic order at finite temperatures that enables scalable spin squeezing.