Exponentially tighter bounds on limitations of quantum error mitigation

Abstract

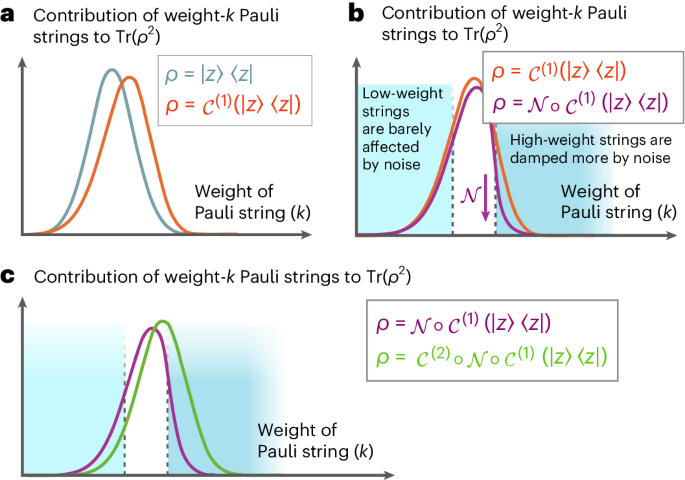
Quantum error mitigation has been proposed as a means to combat unwanted and unavoidable errors in near-term quantum computing without the heavy resource overheads required by fault-tolerant schemes. Recently, error mitigation has been successfully applied to reduce noise in near-term applications. In this work, however, we identify strong limitations to the degree to which quantum noise can be effectively ‘undone’ for larger system sizes. Our framework rigorously captures large classes of error-mitigation schemes in use today. By relating error mitigation to a statistical inference problem, we show that even at shallow circuit depths comparable to those of current experiments, a superpolynomial number of samples is needed in the worst case to estimate the expectation values of noiseless observables, the principal task of error mitigation. Notably, our construction implies that scrambling due to noise can kick in at exponentially smaller depths than previously thought. Noise also impacts other near-term applications by constraining kernel estimation in quantum machine learning, causing an earlier emergence of noise-induced barren plateaus in variational quantum algorithms and ruling out exponential quantum speed-ups in estimating expectation values in the presence of noise or preparing the ground state of a Hamiltonian. Error mitigation has helped improve the performance of current quantum computing devices. Now, a mathematical analysis of the technique suggests its benefits may not extend to larger systems.