Determining intrinsic sensitivity and the role of multiple scattering in speckle metrology
IF 44.8
1区 物理与天体物理
Q1 PHYSICS, APPLIED
引用次数: 0
Abstract
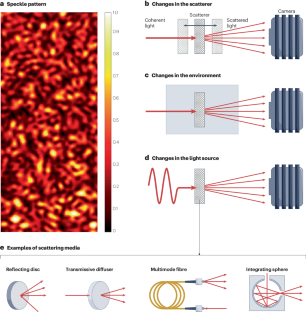
Speckle patterns are a powerful tool for high-precision metrology because they enable remarkable performance in relatively simple setups. Nonetheless, researchers in this field follow rather distinct approaches owing to underappreciated general principles underlying speckle phenomena. For example, speckle can be produced from a simple scatterer or from more complex, multiple scattering geometries. In this Expert Recommendation, we propose a standardization of metrics to quantify intrinsic speckle sensitivity that enables direct comparison between all scattering geometries. Moreover, we provide a general criterion that allows one to predict where multiple scattering is truly advantageous for a given task. This standardization and criterion will catalyse progress in speckle metrology but will also translate to other domains of disordered optics which are undergoing rapid developments at present. Speckle can be harnessed for a wide variety of metrology applications. This Expert Recommendation proposes a standardized metric to allow comparisons of the intrinsic sensitivity of different approaches, and it clarifies when multiple scattering can be beneficial in increasing sensitivity of measurements.

确定斑点计量学的内在灵敏度和多重散射的作用
斑点模式是高精度计量学的强大工具,因为它能在相对简单的设置中实现卓越的性能。然而,由于人们对斑点现象的基本原理认识不足,该领域的研究人员采用了截然不同的方法。例如,斑点可以由简单的散射体产生,也可以由更复杂的多重散射几何体产生。在本专家建议中,我们提出了量化内在斑点灵敏度的标准化指标,可对所有散射几何图形进行直接比较。此外,我们还提供了一个通用标准,可以预测多重散射在特定任务中的真正优势。这种标准化和标准将促进斑点计量学的进步,同时也将转化到目前正在快速发展的无序光学的其他领域。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Nature Reviews Physics
Multiple-
CiteScore
47.80
自引率
0.50%
发文量
122
期刊介绍:
Nature Reviews Physics is an online-only reviews journal, part of the Nature Reviews portfolio of journals. It publishes high-quality technical reference, review, and commentary articles in all areas of fundamental and applied physics. The journal offers a range of content types, including Reviews, Perspectives, Roadmaps, Technical Reviews, Expert Recommendations, Comments, Editorials, Research Highlights, Features, and News & Views, which cover significant advances in the field and topical issues. Nature Reviews Physics is published monthly from January 2019 and does not have external, academic editors. Instead, all editorial decisions are made by a dedicated team of full-time professional editors.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


