Milnor–Wood inequality for klt varieties of general type and uniformization

Abstract

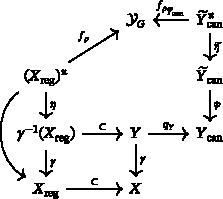
We generalize the definition of the Toledo invariant for representations of fundamental groups of smooth varieties of general type due to Koziarz and Maubon to the context of singular klt varieties, where the natural fundamental groups to consider are those of smooth loci. Assuming that the rank of the target Lie group is not greater than two, we show that the Toledo invariant satisfies a Milnor–Wood-type inequality and we characterize the corresponding maximal representations.