Shortest closed curve to contain a sphere in its convex hull
IF 0.8
3区 数学
Q2 MATHEMATICS
引用次数: 0
Abstract
We show that in Euclidean 3-space any closed curve which contains the unit sphere within its convex hull has length , and characterize the case of equality. This result generalizes the authors' recent solution to a conjecture of Zalgaller. Furthermore, for the analogous problem in dimensions, we include the estimate by Nazarov, which is sharp up to the constant .
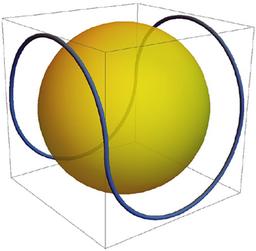
将球面包含在其凸面内的最短闭合曲线
我们证明了在欧几里得三维空间中,任何在其凸壳内包含单位球面的闭合曲线都有长度 L ⩾ 4 π $L\geqslant 4\pi$ ,并描述了相等情况的特征。这一结果概括了作者最近对扎尔加勒猜想的解答。此外,对于 n $n$ 维度的类似问题,我们包含了纳扎罗夫的估计 L ⩾ C n n $L\geqslant Cn\sqrt {n}$,它在常数 C $C$ 的范围内是尖锐的。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
1.90
自引率
0.00%
发文量
198
审稿时长
4-8 weeks
期刊介绍:
Published by Oxford University Press prior to January 2017: http://blms.oxfordjournals.org/

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


