Odd-viscosity induced surfactant-laden shear-imposed viscous film over a slippery incline: a stability analysis

Abstract

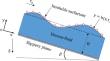
This research focuses on the stability analysis of an odd viscosity-induced shear-imposed Newtonian fluid flowing down an inclined slippery bed having an insoluble surfactant at the top of the liquid surface. The Orr-Sommerfeld boundary value problem is developed by applying the normal mode approach to the infinitesimal perturbed fluid flow and solved using the numerical method Chebyshev spectral collocation. The numerical results confirm the existence of Yih mode and Marangoni mode in the longwave zone. For the clean/contaminated surface of the film flow, the presence of an odd or Hall viscosity coefficient reduces the surface wave energy and delays the transition from laminar to perturbed flow. Also, it has stabilizing nature on the unstable Marangoni mode as well. The growth rate of both clean and contaminated liquid surfaces becomes more/less when the stronger external shear acts along the downstream/upstream direction of fluid flow. Further, the slip parameter leads to a lower critical Reynolds number and makes the liquid surface more unstable. An increase in the critical Reynolds number due to the stronger Marangoni force ensures that the insoluble surfactant has the potential to dampen the Yih mode instability. Moreover, the unstable shear mode occurs in the finite wavenumber regime with very high inertial force and a small angle of inclination. The two-fold variation of the shear mode instability is possible with respect to the imposed shear. However, the inclusion of the odd viscosity coefficient in the viscous falling film may advance the shear mode instability.