Size-Dependent Analysis of Piezoelectric–Elastic Bilayer Microbeams Based on General Strain Gradient Theory

Abstract

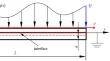
The classical piezoelectric theory fails to capture the size-dependent electromechanical coupling behaviors of piezoelectric microstructures due to the lack of material length-scale parameters. This study presents the constitutive relations of a piezoelectric material in terms of irreducible transversely isotropic tensors that include material length-scale parameters. Using these relations and the general strain gradient theory, a size-dependent bending model is proposed for a bilayer cantilever microbeam consisting of a transversely isotropic piezoelectric layer and an isotropic elastic layer. Analytical solutions are provided for bilayer cantilever microbeams subjected to force load and voltage load. The proposed model can be simplified to the model incorporating only partial strain gradient effects. This study examines the effect of strain gradient by comparing the normalized electric potentials and deflections of different models. Numerical results show that the proposed model effectively captures size effects in piezoelectric microbeams, whereas simplified models underestimate size effects due to ignoring partial strain gradient effects.