Equisingularity in pencils of curves on germs of reduced complex surfaces

Abstract

We study pencils of curves on a germ of complex reduced surface 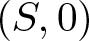$(S,0)$. These are families of curves parametrized by 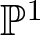$ \mathbb{P}^1 $ having 0 as the unique common point. We prove that for 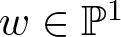$w\in \mathbb{P}^1$, the corresponding curve of the pencil does not have the generic topology if and only if either the corresponding curve of the pulled-back pencil to the normalized surface has a non generic topology or w is a limit value for the function 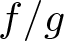$ f/g $ along the singular locus of 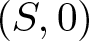$(S,0)$, where f and g are generators of the pencil.