Vector representations and unit vector representations of fields: Problems of understanding and possible teaching strategies

Abstract

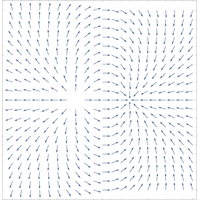
Vector fields are a highly abstract physical concept that is often taught using visualizations. Although vector representations are particularly suitable for visualizing quantitative data, they are often confusing, especially when describing real fields such as magnetic and electric fields, as the vector arrows can overlap. The present study investigates vector understanding at the end of secondary education. In particular, the extent to which the geometry of the field can be derived from conventional unit vector representations and representations with centered unit vectors was examined. To support this understanding, two exercises were compared. The unirepresentational exercise argued within the conventional unit vector representation, while the multirepresentational exercise attempted to support the link between centered and conventional unit vectors. The results show that almost all test subjects solved the items for generating vector representations correctly, but significant difficulties were encountered in interpreting vector representations. Drawing and interpreting vector representations therefore appear to be different skills that should be practiced intensively and in an integrated way. Various problems could be identified when interpreting vector representations. For example, the number of vectors is often erroneously used to estimate the strength of the field, although more vectors per surface element actually only increase the resolution of the representation. Here, however, the results suggest that the longitudinal density and the transverse density of the drawn vectors are perceived differently by the learners. Furthermore, the learners recognized the field’s geometry much more readily from centered unit vectors than from conventional unit vectors. Errors occur especially when interpreting the geometry of conventional unit vector representations of rotational fields and fields containing both sources and sinks while the geometries of fields containing only sinks were interpreted quite well. The comparison between the two training exercises showed that a promising approach to deepen students’ understanding would be to use an exercise that contrasts conventional and centered unit vector representations and explains how to translate from one representation to the other, rather than describing the main elements of only a single representation. Finally, based on the results of the study, we propose a strategy for teaching vector representations in schools. Given the significantly improved readability of the representation with centered unit vectors, the results even raise the question of whether this type of representation could possibly replace the conventional representation in textbooks and learning materials in the future.