On the Smith–Thom deficiency of Hilbert squares
IF 1.1
2区 数学
Q2 MATHEMATICS
引用次数: 0
Abstract
We give an expression for the Smith–Thom deficiency of the Hilbert square of a smooth real algebraic variety in terms of the rank of a suitable Mayer– Vietoris mapping in several situations. As a consequence, we establish a necessary and sufficient condition for the maximality of in the case of projective complete intersections, and show that with a few exceptions, no real nonsingular projective complete intersection of even dimension has maximal Hilbert square. We also provide new examples of smooth real algebraic varieties with maximal Hilbert square.

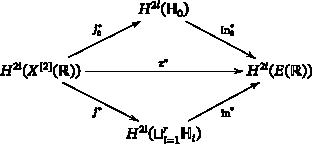
论希尔伯特正方形的史密斯-托姆缺陷
我们给出了几种情况下光滑实代数纷 X $X$ 的希尔伯特平方 X [ 2 ] $X^{[2]}$ 的 Smith-Thom 缺陷的表达式,即合适的 Mayer- Vietoris 映射的秩。因此,在射影完全交的情况下,我们为 X [ 2 ] $X^{[2]}$ 的最大性建立了必要条件和充分条件,并证明除了少数例外,没有偶数维的实非正射完全交具有最大希尔伯特平方。我们还提供了具有最大希尔伯特平方的光滑实代数品种的新例子。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Journal of Topology
数学-数学
CiteScore
2.00
自引率
9.10%
发文量
62
审稿时长
>12 weeks
期刊介绍:
The Journal of Topology publishes papers of high quality and significance in topology, geometry and adjacent areas of mathematics. Interesting, important and often unexpected links connect topology and geometry with many other parts of mathematics, and the editors welcome submissions on exciting new advances concerning such links, as well as those in the core subject areas of the journal.
The Journal of Topology was founded in 2008. It is published quarterly with articles published individually online prior to appearing in a printed issue.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


