Formal model theory and higher topology
IF 0.4
4区 数学
Q4 LOGIC
引用次数: 0
Abstract
We study the 2-categories BIon, of (generalized) bounded ionads, and , of accessible categories with directed colimits, as an abstract framework to approach formal model theory. We relate them to topoi and (lex) geometric sketches, which serve as categorical specifications of geometric theories. We provide reconstruction and completeness-like results. We relate abstract elementary classes to locally decidable topoi. We introduce the notion of categories of saturated objects and relate it to atomic topoi.
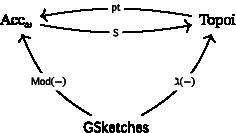
形式模型论和高级拓扑学
我们研究了(广义的)有界离子的二元范畴 BIon 和有向列限的可访问范畴 , 作为接近形式模型理论的抽象框架。我们把它们与作为几何理论分类规范的popoi 和(lex)几何草图联系起来。我们提供了类似重构和完备性的结果。我们将抽象基本类与局部可解拓扑联系起来。我们引入了饱和对象范畴的概念,并将其与原子拓扑联系起来。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
0.60
自引率
0.00%
发文量
49
审稿时长
>12 weeks
期刊介绍:
Mathematical Logic Quarterly publishes original contributions on mathematical logic and foundations of mathematics and related areas, such as general logic, model theory, recursion theory, set theory, proof theory and constructive mathematics, algebraic logic, nonstandard models, and logical aspects of theoretical computer science.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


