Quadratic forms and Genus Theory: A link with 2-descent and an application to nontrivial specializations of ideal classes

IF 16.4 1区化学 Q1 CHEMISTRY, MULTIDISCIPLINARY

Accounts of Chemical Research Pub Date : 2024-05-28 DOI:10.1112/jlms.12921

William Dallaporta

{"title":"Quadratic forms and Genus Theory: A link with 2-descent and an application to nontrivial specializations of ideal classes","authors":"William Dallaporta","doi":"10.1112/jlms.12921","DOIUrl":null,"url":null,"abstract":"Genus Theory is a classical feature of integral binary quadratic forms. Using the author's generalization of the well-known correspondence between quadratic form classes and ideal classes of quadratic algebras, we extend it to the case when quadratic forms are twisted and have coefficients in any principal ideal domain (PID) <math>\n <semantics>\n <mi>R</mi>\n <annotation>$R$</annotation>\n </semantics></math>. When <math>\n <semantics>\n <mrow>\n <mi>R</mi>\n <mo>=</mo>\n <mi>K</mi>\n <mo>[</mo>\n <mi>X</mi>\n <mo>]</mo>\n </mrow>\n <annotation>${R = \\mathbb {K}[X]}$</annotation>\n </semantics></math>, we show that the Genus Theory map is the quadratic form version of the 2-descent map on a certain hyperelliptic curve. As an application, we make a contribution to a question of Agboola and Pappas regarding a specialization problem of divisor classes on hyperelliptic curves. Under suitable assumptions, we prove that the set of nontrivial specializations has density 1.","PeriodicalId":1,"journal":{"name":"Accounts of Chemical Research","volume":null,"pages":null},"PeriodicalIF":16.4000,"publicationDate":"2024-05-28","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1112/jlms.12921","citationCount":"0","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"Accounts of Chemical Research","FirstCategoryId":"100","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1112/jlms.12921","RegionNum":1,"RegionCategory":"化学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"CHEMISTRY, MULTIDISCIPLINARY","Score":null,"Total":0}

引用次数: 0

Abstract

Genus Theory is a classical feature of integral binary quadratic forms. Using the author's generalization of the well-known correspondence between quadratic form classes and ideal classes of quadratic algebras, we extend it to the case when quadratic forms are twisted and have coefficients in any principal ideal domain (PID) $R$ . When $R = K [X]$ , we show that the Genus Theory map is the quadratic form version of the 2-descent map on a certain hyperelliptic curve. As an application, we make a contribution to a question of Agboola and Pappas regarding a specialization problem of divisor classes on hyperelliptic curves. Under suitable assumptions, we prove that the set of nontrivial specializations has density 1.

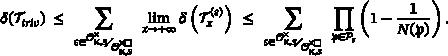
Abstract Image

查看原文本刊更多论文

二次型与属理论：与二阶后裔的联系以及理想类的非琐特殊化应用

属理论是积分二元二次型的一个经典特征。利用作者对二次形式类与二次代数理想类之间著名对应关系的概括，我们将其扩展到二次形式是扭曲的并且在任何主理想域（PID）R $R$ 中都有系数的情况。当 R = K [ X ] ${R = \mathbb {K}[X]}$ 时，我们证明了源论映射是某个超椭圆曲线上 2-descent 映射的二次形式版本。作为应用，我们对阿格博拉和帕帕斯提出的关于超椭圆曲线上除数类的特殊化问题做出了贡献。在适当的假设条件下，我们证明了非小特化集合的密度为 1。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Accounts of Chemical Research 化学-化学综合

CiteScore

31.40

自引率

1.10%

发文量

312

审稿时长

2 months

期刊介绍： Accounts of Chemical Research presents short, concise and critical articles offering easy-to-read overviews of basic research and applications in all areas of chemistry and biochemistry. These short reviews focus on research from the author’s own laboratory and are designed to teach the reader about a research project. In addition, Accounts of Chemical Research publishes commentaries that give an informed opinion on a current research problem. Special Issues online are devoted to a single topic of unusual activity and significance. Accounts of Chemical Research replaces the traditional article abstract with an article "Conspectus." These entries synopsize the research affording the reader a closer look at the content and significance of an article. Through this provision of a more detailed description of the article contents, the Conspectus enhances the article's discoverability by search engines and the exposure for the research.