Nonlinear Dynamics of a Roller Bicycle

IF 0.8 4区数学 Q3 MATHEMATICS, APPLIED

Regular and Chaotic Dynamics Pub Date : 2024-05-06 DOI:10.1134/S1560354724530017

Ivan A. Bizyaev, Ivan S. Mamaev

引用次数: 0

Abstract

In this paper we consider the dynamics of a roller bicycle on a horizontal plane. For this bicycle we derive a nonlinear system of equations of motion in a form that allows us to take into account the symmetry of the system in a natural form. We analyze in detail the stability of straight-line motion depending on the parameters of the bicycle. We find numerical evidence that, in addition to stable straight-line motion, the roller bicycle can exhibit other, more complex, trajectories for which the bicycle does not fall.

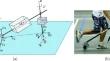
Abstract Image

查看原文本刊更多论文

滚轴自行车的非线性动力学

在本文中，我们考虑了水平面上一辆滚轴自行车的动力学问题。对于这种自行车，我们推导了一个非线性运动方程组，该方程组允许我们以自然的形式考虑系统的对称性。我们详细分析了直线运动的稳定性取决于自行车的参数。我们发现，除了稳定的直线运动外，滚轴自行车还可以表现出其他更复杂的轨迹，在这些轨迹中，自行车不会倒下。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Regular and Chaotic Dynamics 物理-力学

CiteScore

2.50

自引率

7.10%

发文量

审稿时长

>12 weeks

期刊介绍： Regular and Chaotic Dynamics (RCD) is an international journal publishing original research papers in dynamical systems theory and its applications. Rooted in the Moscow school of mathematics and mechanics, the journal successfully combines classical problems, modern mathematical techniques and breakthroughs in the field. Regular and Chaotic Dynamics welcomes papers that establish original results, characterized by rigorous mathematical settings and proofs, and that also address practical problems. In addition to research papers, the journal publishes review articles, historical and polemical essays, and translations of works by influential scientists of past centuries, previously unavailable in English. Along with regular issues, RCD also publishes special issues devoted to particular topics and events in the world of dynamical systems.