Complete classification of planar p-elasticae
IF 1
3区 数学
Q1 MATHEMATICS
引用次数: 0
Abstract
Euler’s elastica is defined by a critical point of the total squared curvature under the fixed length constraint, and its \(L^p\)-counterpart is called p-elastica. In this paper we completely classify all p-elasticae in the plane and obtain their explicit formulae as well as optimal regularity. To this end we introduce new types of p-elliptic functions which streamline the whole argument and result. As an application we also classify all closed planar p-elasticae.
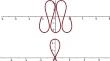
平面 p-elasticae 的完整分类
欧拉弹性是由固定长度约束下总曲率平方的临界点定义的,它的(L^p\)对应物被称为 p-弹性。在本文中,我们对平面内的所有 p-elasticae 进行了完全分类,并得到了它们的显式以及最优正则性。为此,我们引入了新型 p-elliptic 函数,简化了整个论证和结果。作为应用,我们还对所有封闭的平面 p-elasticae 进行了分类。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
2.10
自引率
10.00%
发文量
99
审稿时长
>12 weeks
期刊介绍:
This journal, the oldest scientific periodical in Italy, was originally edited by Barnaba Tortolini and Francesco Brioschi and has appeared since 1850. Nowadays it is managed by a nonprofit organization, the Fondazione Annali di Matematica Pura ed Applicata, c.o. Dipartimento di Matematica "U. Dini", viale Morgagni 67A, 50134 Firenze, Italy, e-mail annali@math.unifi.it).
A board of Italian university professors governs the Fondazione and appoints the editors of the journal, whose responsibility it is to supervise the refereeing process. The names of governors and editors appear on the front page of each issue. Their addresses appear in the title pages of each issue.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


