Stray field computation by inverted finite elements: a new method in micromagnetic simulations

IF 1.7 3区数学 Q2 MATHEMATICS, APPLIED

Advances in Computational Mathematics Pub Date : 2024-05-07 DOI:10.1007/s10444-024-10139-2

Tahar Z. Boulmezaoud, Keltoum Kaliche

引用次数: 0

Abstract

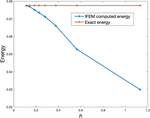
In this paper, we propose a new method for computing the stray-field and the corresponding energy for a given magnetization configuration. Our approach is based on the use of inverted finite elements and does not need any truncation. After analyzing the problem in an appropriate functional framework, we describe the method and we prove its convergence. We then display some computational results which demonstrate its efficiency and confirm its full potential.

Abstract Image

查看原文本刊更多论文

用倒置有限元计算杂散场：微磁模拟中的一种新方法

在本文中，我们提出了一种计算给定磁化配置的杂散磁场和相应能量的新方法。我们的方法基于倒置有限元的使用，不需要任何截断。在适当的函数框架下分析问题后，我们描述了该方法，并证明了其收敛性。然后，我们展示了一些计算结果，这些结果证明了该方法的效率，并证实了它的全部潜力。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Advances in Computational Mathematics 数学-应用数学

CiteScore

3.00

自引率

5.90%

发文量

审稿时长

3 months

期刊介绍： Advances in Computational Mathematics publishes high quality, accessible and original articles at the forefront of computational and applied mathematics, with a clear potential for impact across the sciences. The journal emphasizes three core areas: approximation theory and computational geometry; numerical analysis, modelling and simulation; imaging, signal processing and data analysis. This journal welcomes papers that are accessible to a broad audience in the mathematical sciences and that show either an advance in computational methodology or a novel scientific application area, or both. Methods papers should rely on rigorous analysis and/or convincing numerical studies.