Error estimation for non-linear singularly perturbed reaction–diffusion parabolic problems via element-free Galerkin method
Abstract
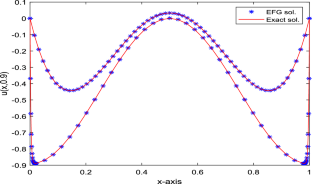
The current study aims to develop an error analysis for non-linear parabolic singularly perturbed reaction–diffusion problems using element-free Galerkin method. A robust numerical methodology is introduced based on combining the implicit Crank–Nicolson scheme for temporal derivatives and the element-free Galerkin (EFG) method for spatial derivatives. The moving least-squares (MLS) approximation has been employed to generate the shape functions. Essential boundary conditions have been enforced by the incorporation of the Lagrange multiplier method. Due to the presence of steep boundary layers in the solution of the considered problem, a piecewise-uniform layer-adapted Shishkin’s technique has been used to generate nodal points at the transition point. The stability and error analysis of the present method on a discrete \(L^{2}-\)norm is analyzed in an innovative theoretical framework. The \(\epsilon\)-uniform convergency of the fully-discrete EFG method is shown to be \(\mathcal {O}(\tau ^{2}+d_{s}^{m})\), where \(\tau\) and \(d_{s}^{m}\) are the time step size and size of the influence domain, respectively. The Lagrange multiplier method has been incorporated to deal with the implementation of essential boundary conditions. Lastly, a few numerical experiments are performed to validate the theoretical results and verify the computational consistency and robustness of the proposed scheme. The \(L_{\infty }\) errors and the convergence rate have been presented.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


