Logarithmic Donaldson–Thomas theory

Abstract

Let X be a smooth and projective threefold with a simple normal crossings divisor D. We construct the Donaldson–Thomas theory of the pair 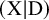$(X|D)$ enumerating ideal sheaves on X relative to D. These moduli spaces are compactified by studying subschemes in expansions of the target geometry, and the moduli space carries a virtual fundamental class leading to numerical invariants with expected properties. We formulate punctual evaluation, rationality and wall-crossing conjectures, in parallel with the standard theory. Our formalism specializes to the Li–Wu theory of relative ideal sheaves when the divisor is smooth and is parallel to recent work on logarithmic Gromov–Witten theory with expansions.