2D Dilaton Gravity and the Weil–Petersson Volumes with Conical Defects
IF 2.6
1区 物理与天体物理
Q1 PHYSICS, MATHEMATICAL
引用次数: 0
Abstract
We derive the Weil–Petersson measure on the moduli space of hyperbolic surfaces with defects of arbitrary opening angles and use this to compute its volume. We conjecture a matrix integral computing the corresponding volumes and confirm agreement in simple cases. We combine this mathematical result with the equivariant localization approach to Jackiw–Teitelboim gravity to justify a proposed exact solution of pure 2d dilaton gravity for a large class of dilaton potentials.
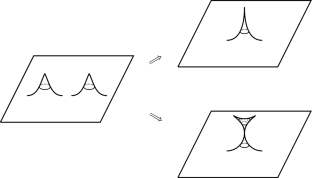

具有锥形缺陷的二维迪拉顿引力和魏尔-彼得森卷
我们推导出具有任意开口角缺陷的双曲面模空间上的魏尔-彼得森度量,并以此计算其体积。我们猜想了计算相应体积的矩阵积分,并确认了在简单情况下的一致性。我们将这一数学结果与杰克维-泰特博伊姆引力的等变局部化方法结合起来,证明了针对一大类稀拉顿势提出的纯二维稀拉顿引力精确解的合理性。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Communications in Mathematical Physics
物理-物理:数学物理
CiteScore
4.70
自引率
8.30%
发文量
226
审稿时长
3-6 weeks
期刊介绍:
The mission of Communications in Mathematical Physics is to offer a high forum for works which are motivated by the vision and the challenges of modern physics and which at the same time meet the highest mathematical standards.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


