Stochastic Quantification of Spatial Variability of Flow Fields in Heterogeneous, Non-uniform, Confined Aquifers
Abstract
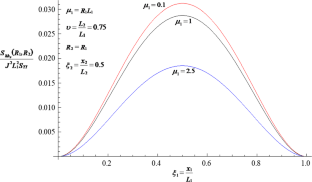
Stochastic quantification of flow field variability in complex geologic formations under uncertainty is expected to provide valuable information for rational management of regional groundwater resources and analysis of solute transport processes for stochastic environmental risk assessment. Studies of fluid flow behavior in confined aquifers of variable thickness presented in the literature assume that the thickness of the aquifer varies linearly or nonlinearly. However, natural variations, such as the thickness of the aquifer caused by complex natural events, cannot be accurately predicted. Therefore, quantifying the variability of the flow field in heterogeneous, non-uniform, confined aquifers may be done from a stochastic perspective. In this study, the spatial variations in hydraulic conductivity are considered as a stationary random process, while the spatial variations in aquifer thickness are treated as a nonstationary random process with homogeneous (stationary) increments. General expressions for the spatial covariance functions and the evolutionary power spectra of the depth-averaged hydraulic head and integrated specific discharge in the direction of x1 are derived using the Fourier–Stieltjes spectral representation approach and representation theorem. Closed-form solutions for the evolutionary power spectra of depth-averaged hydraulic head and integrated specific discharge are used to analyze the effect of variation in the thickness of the confined aquifer on the variability of depth-averaged head and integrated discharge. An application of the theory developed here to the case of random aquifer thickness fields exhibiting a power-law semivariogram is given. The results of this study improve the understanding and quantification of flow field variability in natural confined aquifers.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


