Limit Cycle Bifurcations Near Nonsmooth Homoclinic Cycle in Discontinuous Systems

IF 16.4 1区化学 Q1 CHEMISTRY, MULTIDISCIPLINARY

Accounts of Chemical Research Pub Date : 2024-03-25 DOI:10.1007/s10884-024-10358-7

Duo Hua, Xingbo Liu

引用次数: 0

Abstract

The main aim of this paper is to study the limit cycle bifurcations near the homoclinic cycle in the discontinuous systems. Based on the impoved Lin’s method, we establish the bifurcation equation, which presents the existence of limit cycles bifurcated from nonsmooth homoclinic cycles under perturbation. Furthermore, we give an example to support our conclusions. After solving a boundary value problem with numerical tools, we provide the exact parameter values for the system having a limit cycle.

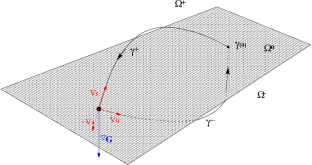
Abstract Image

查看原文本刊更多论文

非连续系统中接近非光滑同线性周期的极限周期分岔

本文的主要目的是研究不连续系统中同轴周期附近的极限周期分岔。基于林氏方法，我们建立了分岔方程，提出了在扰动下由非光滑同线性周期分岔而来的极限周期的存在性。此外，我们还举了一个例子来支持我们的结论。利用数值工具求解边界值问题后，我们提供了具有极限循环的系统的精确参数值。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Accounts of Chemical Research 化学-化学综合

CiteScore

31.40

自引率

1.10%

发文量

312

审稿时长

2 months

期刊介绍： Accounts of Chemical Research presents short, concise and critical articles offering easy-to-read overviews of basic research and applications in all areas of chemistry and biochemistry. These short reviews focus on research from the author’s own laboratory and are designed to teach the reader about a research project. In addition, Accounts of Chemical Research publishes commentaries that give an informed opinion on a current research problem. Special Issues online are devoted to a single topic of unusual activity and significance. Accounts of Chemical Research replaces the traditional article abstract with an article "Conspectus." These entries synopsize the research affording the reader a closer look at the content and significance of an article. Through this provision of a more detailed description of the article contents, the Conspectus enhances the article's discoverability by search engines and the exposure for the research.