Thermo-mechanical waves in a biological tissue under ramp and oscillatory heat in Atangana–Baleanu fractional theory

Abstract

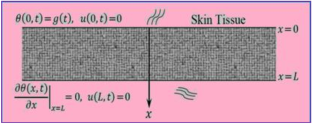
Accurate outcome prediction in a thermal treatment of a biological tissue is challenging for the medical practitioners. This paper makes an attempt to predict the outcomes using fractional modelling of the heat transfer. The model has the capability to describe the characteristics in the transient heat transport in a biological tissue. A novel heat transfer model is established with two relaxation times in the Atangana and Baleanu fractional derivatives. A comparison of the thermo-mechanical waves originated inside the skin tissue was made for the ramp and harmonic heat. Laplace transform is performed to obtain the analytical solution of dimensionless temperature, dilation, displacement, and thermal stress. Effects of the fractional parameters and the time are evaluated through the graphical results for both types of heat input. Auspicious outcomes are noticed for the different thermal loadings. Results under sinusoidal heat are observed to be stable compared to the results under ramp heat. Moreover, graphical results of the physical quantities under Atangana–Baleanu fractional model are compared with the results for the conventional dual phase lag model having integer-order derivatives. Results under fractional theory provide compressed values of the physical fields and prevent the damage formation inside the tissue. The paper provides a technique suitable for outcome prediction by medical practitioners in thermal therapy for diseases such as cancer and hyperthermia.