Robustness analysis of exponential stability of fuzzy inertial neural networks through the estimation of upper limits of perturbations

IF 2.6 4区计算机科学 Q3 COMPUTER SCIENCE, ARTIFICIAL INTELLIGENCE

Neural Processing Letters Pub Date : 2024-03-20 DOI:10.1007/s11063-024-11587-z

Wenxiang Fang, Tao Xie

引用次数: 0

Abstract

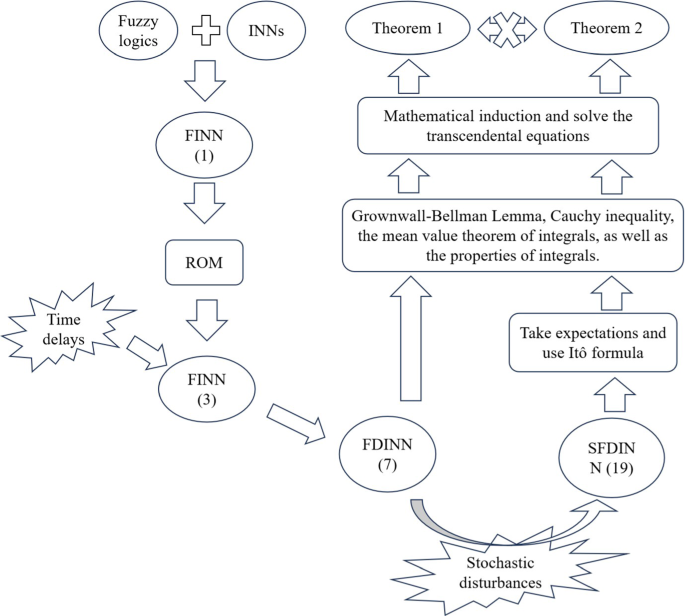
This paper characterizes the robustness of exponential stability of fuzzy inertial neural network which contains time delays or stochastic disturbance through the estimation of upper limits of perturbations. By utilizing Gronwall-Bellman lemma, stochastic analysis, Cauchy inequality, the mean value theorem of integrals, as well as the properties of integrations, the limits of both time delays and stochastic disturbances are derived in this paper which can make the disturbed system keep exponential stability. The constraints between the two types of disturbances are provided in this paper. Examples are offered to validate our results.

Abstract Image

查看原文本刊更多论文

通过估计扰动上限对模糊惯性神经网络指数稳定性的稳健性分析

本文通过对扰动上限的估计，描述了包含时间延迟或随机扰动的模糊惯性神经网络指数稳定性的鲁棒性。本文利用 Gronwall-Bellman Lemma、随机分析、Cauchy 不等式、积分均值定理以及积分的性质，推导出时间延迟和随机扰动的极限，从而使受扰动系统保持指数稳定性。本文提供了两种扰动之间的约束条件。本文举例验证了我们的结果。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Neural Processing Letters 工程技术-计算机：人工智能

CiteScore

4.90

自引率

12.90%

发文量

392

审稿时长

2.8 months

期刊介绍： Neural Processing Letters is an international journal publishing research results and innovative ideas on all aspects of artificial neural networks. Coverage includes theoretical developments, biological models, new formal modes, learning, applications, software and hardware developments, and prospective researches. The journal promotes fast exchange of information in the community of neural network researchers and users. The resurgence of interest in the field of artificial neural networks since the beginning of the 1980s is coupled to tremendous research activity in specialized or multidisciplinary groups. Research, however, is not possible without good communication between people and the exchange of information, especially in a field covering such different areas; fast communication is also a key aspect, and this is the reason for Neural Processing Letters