Asymptotical stabilization of fuzzy semilinear dynamic systems involving the generalized Caputo fractional derivative for $$q \in (1,2)$$
IF 4.6
Q2 MATERIALS SCIENCE, BIOMATERIALS
引用次数: 0
Abstract
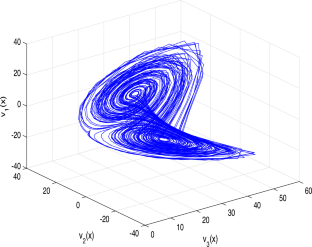
In this study, the asymptotical stabilization problem of fuzzy fractional dynamic systems (FFDSs) with the semilinear form under the granular Caputo fractional derivative for the case \(q \in (1,2)\) is investigated. To tackle this, we propose a linear feedback controller aimed at stabilizing the unstable states of FFDSs. Taking advantage of the generalized fractional Laplace-like transform (GFLT) and the Gronwall-Bellman inequality, we provide a simple method to evaluate the stability of fractional dynamical systems. Finally, we validate the effectiveness of our approach through examples and corresponding simulations.
涉及 $$q \ in (1,2)$$ 的广义卡普托分数导数的模糊半线性动态系统的渐近稳定问题
在本研究中,我们研究了在粒状卡普托分数导数下具有半线性形式的模糊分数动态系统(FFDSs)在 \(q \in (1,2)\) 情况下的渐近稳定问题。为此,我们提出了一种线性反馈控制器,旨在稳定 FFDSs 的不稳定状态。利用广义分数拉普拉斯变换(GFLT)和 Gronwall-Bellman 不等式,我们提供了一种评估分数动力系统稳定性的简单方法。最后,我们通过实例和相应的模拟验证了我们方法的有效性。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


