Unit sphere fibrations in Euclidean space

Abstract

We show that if an open set in 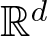$\mathbb{R}^d$ can be fibered by unit n-spheres, then 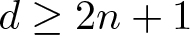$d \geq 2n+1$, and if 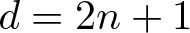$d = 2n+1$, then the spheres must be pairwise linked, and 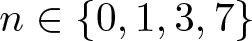$n \in \left\{0, 1, 3, 7 \right\}$. For these values of n, we construct unit n-sphere fibrations in 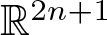$\mathbb{R}^{2n+1}$.