RADU GROUPS ACTING ON TREES ARE CCR

Abstract

We classify the irreducible unitary representations of closed simple groups of automorphisms of trees acting 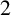$2$-transitively on the boundary and whose local action at every vertex contains the alternating group. As an application, we confirm Claudio Nebbia’s CCR conjecture on trees for 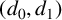$(d_0,d_1)$-semi-regular trees such that 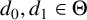$d_0,d_1\in \Theta $, where $\Theta $ is an asymptotically dense set of positive integers.