Employment of an efficient particle tracking algorithm based on barycentric coordinates in hybrid finite‐volume/probability‐density‐function Monte Carlo methods
IF 1.7
4区 工程技术
Q3 COMPUTER SCIENCE, INTERDISCIPLINARY APPLICATIONS
引用次数: 0
Abstract
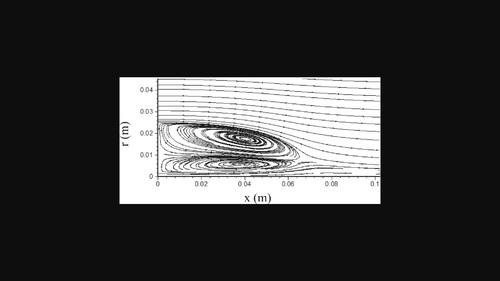
One main concern of this work is to develop an efficient particle‐tracking‐managing algorithm in the framework of a hybrid pressure‐based finite‐volume/probability‐density‐function (FV/PDF) Monte‐Carlo (MC) solution algorithm to extend the application of FV/PDF MC methods to absolutely incompressible flows and speedup the convergence rate of solving the fluctuating velocity‐turbulent frequency joint PDF equation in turbulent flow simulations. Contrary to the density‐based algorithms, the pressure‐based algorithms have stable convergence rates even in zero‐Mach number flows. As another contribution, literature shows that the past developed methods mostly used mesh searching techniques to attribute particles to cells at the beginning of each tracking time‐step. Also, they had to calculate the linear basis functions at every time‐step to estimate the particle mean fields and interpolate the data. These calculations would be computationally very expensive, time‐consuming, and inefficient in computational domains with arbitrary‐shaped 3D meshes. As known, the barycentric tracking is a continuous particle tracking method, which provides more efficiency in case of handling 3D domains with general mesh shapes. The barycentric tracking eliminates any mesh searching technique and readily provides the convenient linear basis functions. So, this work benefits from these advantages and tracks the particles based on their barycentric coordinates. It leads to less computational work and a better efficiency for the present method. A bluff‐body turbulent flow case is examined to validate the present FV/PDF MC method. From the accuracy perspective, it is shown that the results of the present algorithm are in great agreement with experimental data and available numerical solutions. The present study shows that the number of particle time‐steps required to reach the statistically steady‐state condition is at least one‐sixth less than the previously developed algorithms. This also approves a faster convergence rate for the present hybrid pressure‐based algorithm.
在有限体积/概率密度函数蒙特卡罗混合方法中采用基于重心坐标的高效粒子跟踪算法
这项工作的主要关注点之一是在基于压力的有限体积/概率密度函数(FV/PDF)混合蒙特卡洛(MC)求解算法框架内开发一种高效的粒子跟踪管理算法,以将 FV/PDF MC 方法的应用扩展到绝对不可压缩流,并加快湍流模拟中波动速度-湍流频率联合 PDF 方程求解的收敛速度。与基于密度的算法相反,基于压力的算法即使在零马赫数流动中也有稳定的收敛率。另一个贡献是,文献显示,过去开发的方法大多使用网格搜索技术,在每个跟踪时间步开始时将粒子归属到单元。此外,他们还必须在每个时间步计算线性基函数,以估计粒子平均场并对数据进行插值。在具有任意形状三维网格的计算域中,这些计算将非常昂贵、耗时和低效。众所周知,双曲跟踪是一种连续粒子跟踪方法,在处理具有一般网格形状的三维域时效率更高。双曲跟踪消除了任何网格搜索技术,并能提供方便的线性基函数。因此,这项工作得益于这些优势,并根据粒子的偏心坐标对其进行跟踪。 这使得本方法的计算工作量更少,效率更高。为了验证本 FV/PDF MC 方法,我们研究了一个崖体湍流案例。从精度角度来看,本算法的结果与实验数据和现有数值解非常一致。本研究表明,达到统计稳态条件所需的粒子时间步数比以前开发的算法至少少六分之一。这也证明本基于压力的混合算法收敛速度更快。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
3.70
自引率
5.60%
发文量
111
审稿时长
8 months
期刊介绍:
The International Journal for Numerical Methods in Fluids publishes refereed papers describing significant developments in computational methods that are applicable to scientific and engineering problems in fluid mechanics, fluid dynamics, micro and bio fluidics, and fluid-structure interaction. Numerical methods for solving ancillary equations, such as transport and advection and diffusion, are also relevant. The Editors encourage contributions in the areas of multi-physics, multi-disciplinary and multi-scale problems involving fluid subsystems, verification and validation, uncertainty quantification, and model reduction.
Numerical examples that illustrate the described methods or their accuracy are in general expected. Discussions of papers already in print are also considered. However, papers dealing strictly with applications of existing methods or dealing with areas of research that are not deemed to be cutting edge by the Editors will not be considered for review.
The journal publishes full-length papers, which should normally be less than 25 journal pages in length. Two-part papers are discouraged unless considered necessary by the Editors.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


