Some rational homology computations for diffeomorphisms of odd-dimensional manifolds
IF 1.1
2区 数学
Q2 MATHEMATICS
引用次数: 0
Abstract
We calculate the rational cohomology of the classifying space of the diffeomorphism group of the manifolds , for large and , up to degree . The answer is that it is a free graded commutative algebra on an appropriate set of Miller–Morita–Mumford classes. Our proof goes through the classical three-step procedure: (a) compute the cohomology of the homotopy automorphisms, (b) use surgery to compare this to block diffeomorphisms, and (c) use pseudoisotopy theory and algebraic -theory to get at actual diffeomorphism groups.

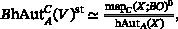
奇维流形差分同调的一些理性同调计算
我们计算流形差分群分类空间的有理同调 U g , 1 n : = # g ( S n × S n + 1 ) ∖ int ( D 2 n + 1 ) $U_{g,1}^n:= \#^g(S^n \times S^{n+1})\setminus \mathrm{int}(D^{2n+1})$,对于大g $g$和n $n$,直到度数n - 3 $n-3$。答案是,它是一个在适当的米勒-莫里塔-蒙福德类集合上的自由分级交换代数。我们的证明经历了经典的三步程序:(a) 计算同调自形体的同调;(b) 利用外科手术将其与块差形体进行比较;(c) 利用伪拟态理论和代数 K $K$ 理论得到实际的差形群。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Journal of Topology
数学-数学
CiteScore
2.00
自引率
9.10%
发文量
62
审稿时长
>12 weeks
期刊介绍:
The Journal of Topology publishes papers of high quality and significance in topology, geometry and adjacent areas of mathematics. Interesting, important and often unexpected links connect topology and geometry with many other parts of mathematics, and the editors welcome submissions on exciting new advances concerning such links, as well as those in the core subject areas of the journal.
The Journal of Topology was founded in 2008. It is published quarterly with articles published individually online prior to appearing in a printed issue.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


