PL-Genus of surfaces in homology balls

Abstract

We consider manifold-knot pairs 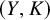$(Y,K)$, where Y is a homology 3-sphere that bounds a homology 4-ball. We show that the minimum genus of a PL surface 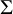$\Sigma $ in a homology ball X, such that $\partial (X, \Sigma ) = (Y, K)$ can be arbitrarily large. Equivalently, the minimum genus of a surface cobordism in a homology cobordism from 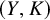$(Y, K)$ to any knot in 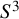$S^3$ can be arbitrarily large. The proof relies on Heegaard Floer homology.