Tropical Fock–Goncharov coordinates for -webs on surfaces I: construction

Abstract

For a finite-type surface $\mathfrak {S}$, we study a preferred basis for the commutative algebra $\mathbb {C}[\mathscr {R}_{\mathrm {SL}_3(\mathbb {C})}(\mathfrak {S})]$ of regular functions on the 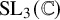$\mathrm {SL}_3(\mathbb {C})$-character variety, introduced by Sikora–Westbury. These basis elements come from the trace functions associated to certain trivalent graphs embedded in the surface $\mathfrak {S}$. We show that this basis can be naturally indexed by nonnegative integer coordinates, defined by Knutson–Tao rhombus inequalities and modulo 3 congruence conditions. These coordinates are related, by the geometric theory of Fock and Goncharov, to the tropical points at infinity of the dual version of the character variety.