Stabilization of Steady Rotations of a Spherical Robot on a Vibrating Base Using Feedback
IF 0.8
4区 数学
Q3 MATHEMATICS, APPLIED
引用次数: 0
Abstract
This paper treats the problem of a spherical robot with an axisymmetric pendulum drive rolling without slipping on a vibrating plane. The main purpose of the paper is to investigate the stabilization of the upper vertical rotations of the pendulum using feedback (additional control action). For the chosen type of feedback, regions of asymptotic stability of the upper vertical rotations of the pendulum are constructed and possible bifurcations are analyzed. Special attention is also given to the question of the stability of periodic solutions arising as the vertical rotations lose stability.
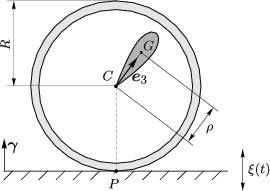
利用反馈稳定振动底座上球形机器人的稳定旋转
本文讨论了一个带有轴对称摆锤驱动器的球形机器人在振动平面上无滑动运行的问题。本文的主要目的是利用反馈(附加控制作用)研究摆锤上部垂直旋转的稳定性。对于所选的反馈类型,本文构建了摆锤上部垂直旋转的渐近稳定区域,并分析了可能出现的分岔。还特别关注了随着垂直旋转失去稳定性而产生的周期解的稳定性问题。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
2.50
自引率
7.10%
发文量
35
审稿时长
>12 weeks
期刊介绍:
Regular and Chaotic Dynamics (RCD) is an international journal publishing original research papers in dynamical systems theory and its applications. Rooted in the Moscow school of mathematics and mechanics, the journal successfully combines classical problems, modern mathematical techniques and breakthroughs in the field. Regular and Chaotic Dynamics welcomes papers that establish original results, characterized by rigorous mathematical settings and proofs, and that also address practical problems. In addition to research papers, the journal publishes review articles, historical and polemical essays, and translations of works by influential scientists of past centuries, previously unavailable in English. Along with regular issues, RCD also publishes special issues devoted to particular topics and events in the world of dynamical systems.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


