ON THE ALGEBRAS

Abstract

Let H be an ultraspherical hypergroup and let 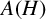$A(H)$ be the Fourier algebra associated with 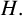$H.$ In this paper, we study the dual and the double dual of 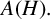$A(H).$ We prove among other things that the subspace of all uniformly continuous functionals on 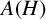$A(H)$ forms a 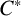$C^*$-algebra. We also prove that the double dual 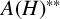$A(H)^{\ast \ast }$ is neither commutative nor semisimple with respect to the Arens product, unless the underlying hypergroup H is finite. Finally, we study the unit elements of 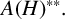$A(H)^{\ast \ast }.$