A Topology-Shape-Metrics Framework for Ortho-Radial Graph Drawing

Abstract

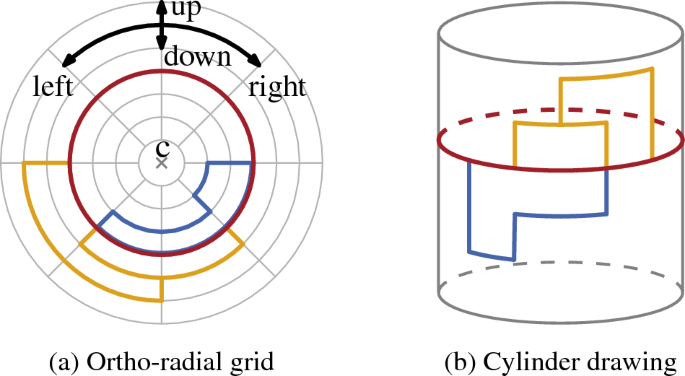
Abstract Orthogonal drawings, i.e., embeddings of graphs into grids, are a classic topic in Graph Drawing. Often the goal is to find a drawing that minimizes the number of bends on the edges. A key ingredient for bend minimization algorithms is the existence of an orthogonal representation that allows to describe such drawings purely combinatorially by only listing the angles between the edges around each vertex and the directions of bends on the edges, but neglecting any kind of geometric information such as vertex coordinates or edge lengths. In this work, we generalize this idea to ortho-radial representations of ortho-radial drawings , which are embeddings into an ortho-radial grid, whose gridlines are concentric circles around the origin and straight-line spokes emanating from the origin but excluding the origin itself. Unlike the orthogonal case, there exist ortho-radial representations that do not admit a corresponding drawing, for example so-called strictly monotone cycles. An ortho-radial representation is called valid if it does not contain a strictly monotone cycle. Our first main result is that an ortho-radial representation admits a corresponding drawing if and only if it is valid. Previously such a characterization was only known for ortho-radial drawings of paths, cycles, and theta graphs (Hasheminezhad et al. in Australas J Combin 44:171–182, 2009), and in the special case of rectangular drawings of cubic graphs (Hasheminezhad et al. in Comput Geom 43(9):767–780, 2010), where the contour of each face is required to be a combinatorial rectangle. Additionally, we give a quadratic-time algorithm that tests for a given ortho-radial representation whether it is valid, and we show how to draw a valid ortho-radial representation in the same running time. Altogether, this reduces the problem of computing a minimum-bend ortho-radial drawing to the task of computing a valid ortho-radial representation with the minimum number of bends, and hence establishes an ortho-radial analogue of the topology-shape-metrics framework for planar orthogonal drawings by Tamassia (SIAM J Comput 16(3):421–444, 1987).