About the performance of perturbative treatments of the spin-boson dynamics within the hierarchical equations of motion approach
IF 2.3
3区 物理与天体物理
Q2 PHYSICS, MULTIDISCIPLINARY
引用次数: 0
Abstract
Abstract The hierarchical equations of motion (HEOM) provide a numerically exact approach for simulating the dynamics of open quantum systems coupled to a harmonic bath. However, its applicability has traditionally been limited to specific spectral forms and relatively high temperatures. Recently, an extended version called Free-Pole HEOM (FP-HEOM) has been developed to overcome these limitations. In this study, we demonstrate that the FP-HEOM method can be systematically employed to investigate higher order master equations by truncating the FP-HEOM hierarchy at a desired tier. We focus on the challenging scenario of the spin-boson problem with a sub-Ohmic spectral distribution at zero temperature and analyze the performance of the corresponding master equations. Furthermore, we compare the memory kernel for population dynamics obtained from the exact FP-HEOM dynamics with that of the approximate Non-Interacting-Blip Approximation (NIBA).
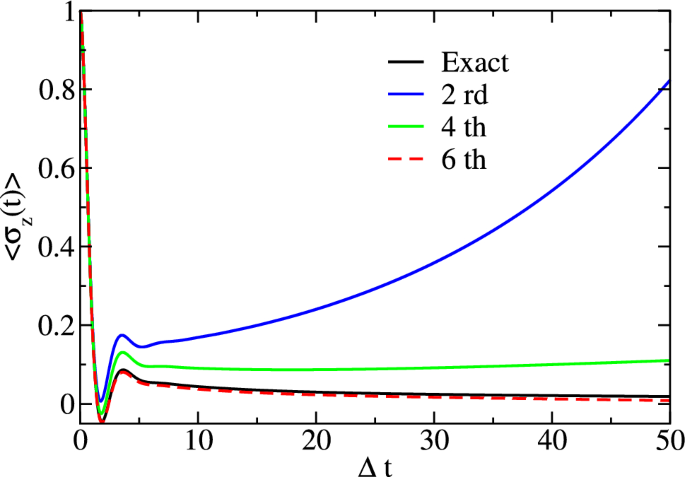
关于自旋玻色子动力学在层次运动方程中的微扰处理的性能
层次运动方程(HEOM)为模拟开放量子系统与谐波槽耦合的动力学提供了一种精确的数值方法。然而,它的适用性传统上仅限于特定的光谱形式和相对较高的温度。最近,一种名为自由极HEOM (FP-HEOM)的扩展版本已经开发出来,以克服这些限制。在这项研究中,我们证明了FP-HEOM方法可以系统地用于研究高阶主方程,通过在期望的层上截断FP-HEOM层次。重点研究了零温度下具有亚欧姆谱分布的自旋玻色子问题的挑战性场景,并分析了相应的主方程的性能。此外,我们比较了从精确的FP-HEOM动力学得到的种群动力学的记忆核与近似的非相互作用-光点近似(NIBA)的记忆核。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
5.10
自引率
10.70%
发文量
313
审稿时长
3-8 weeks
期刊介绍:
EPJ - Special Topics (EPJ ST) publishes topical issues which are collections of review-type articles or extensive, detailed progress reports. Each issue is focused on a specific subject matter of topical interest.
The journal scope covers the whole spectrum of pure and applied physics, including related subjects such as Materials Science, Physical Biology, Physical Chemistry, and Complex Systems with particular emphasis on interdisciplinary topics in physics and related fields.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


