Generalized Pitchfork Bifurcations in D-Concave Nonautonomous Scalar Ordinary Differential Equations

IF 16.4 1区化学 Q1 CHEMISTRY, MULTIDISCIPLINARY

Accounts of Chemical Research Pub Date : 2023-09-23 DOI:10.1007/s10884-023-10309-8

Jesús Dueñas, Carmen Núñez, Rafael Obaya

{"title":"Generalized Pitchfork Bifurcations in D-Concave Nonautonomous Scalar Ordinary Differential Equations","authors":"Jesús Dueñas, Carmen Núñez, Rafael Obaya","doi":"10.1007/s10884-023-10309-8","DOIUrl":null,"url":null,"abstract":"Abstract The global bifurcation diagrams for two different one-parametric perturbations ( $$+\\lambda x$$ <mml:math xmlns:mml=\"http://www.w3.org/1998/Math/MathML\"> <mml:mrow> <mml:mo>+</mml:mo> <mml:mi>λ</mml:mi> <mml:mi>x</mml:mi> </mml:mrow> </mml:math> and $$+\\lambda x^2$$ <mml:math xmlns:mml=\"http://www.w3.org/1998/Math/MathML\"> <mml:mrow> <mml:mo>+</mml:mo> <mml:mi>λ</mml:mi> <mml:msup> <mml:mi>x</mml:mi> <mml:mn>2</mml:mn> </mml:msup> </mml:mrow> </mml:math> ) of a dissipative scalar nonautonomous ordinary differential equation $$x'=f(t,x)$$ <mml:math xmlns:mml=\"http://www.w3.org/1998/Math/MathML\"> <mml:mrow> <mml:msup> <mml:mi>x</mml:mi> <mml:mo>′</mml:mo> </mml:msup> <mml:mo>=</mml:mo> <mml:mi>f</mml:mi> <mml:mrow> <mml:mo>(</mml:mo> <mml:mi>t</mml:mi> <mml:mo>,</mml:mo> <mml:mi>x</mml:mi> <mml:mo>)</mml:mo> </mml:mrow> </mml:mrow> </mml:math> are described assuming that 0 is a constant solution, that f is recurrent in t , and that its first derivative with respect to x is a strictly concave function. The use of the skewproduct formalism allows us to identify bifurcations with changes in the number of minimal sets and in the shape of the global attractor. In the case of perturbation $$+\\lambda x$$ <mml:math xmlns:mml=\"http://www.w3.org/1998/Math/MathML\"> <mml:mrow> <mml:mo>+</mml:mo> <mml:mi>λ</mml:mi> <mml:mi>x</mml:mi> </mml:mrow> </mml:math> , a so-called generalized pitchfork bifurcation may arise, with the particularity of lack of an analogue in autonomous dynamics. This new bifurcation pattern is extensively investigated in this work.","PeriodicalId":1,"journal":{"name":"Accounts of Chemical Research","volume":null,"pages":null},"PeriodicalIF":16.4000,"publicationDate":"2023-09-23","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"2","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"Accounts of Chemical Research","FirstCategoryId":"1085","ListUrlMain":"https://doi.org/10.1007/s10884-023-10309-8","RegionNum":1,"RegionCategory":"化学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"CHEMISTRY, MULTIDISCIPLINARY","Score":null,"Total":0}

引用次数: 2

Abstract

Abstract The global bifurcation diagrams for two different one-parametric perturbations ( $$+\lambda x$$ + λ x and $$+\lambda x^2$$ + λ x 2 ) of a dissipative scalar nonautonomous ordinary differential equation $$x'=f(t,x)$$ x ′ = f ( t , x ) are described assuming that 0 is a constant solution, that f is recurrent in t , and that its first derivative with respect to x is a strictly concave function. The use of the skewproduct formalism allows us to identify bifurcations with changes in the number of minimal sets and in the shape of the global attractor. In the case of perturbation $$+\lambda x$$ + λ x , a so-called generalized pitchfork bifurcation may arise, with the particularity of lack of an analogue in autonomous dynamics. This new bifurcation pattern is extensively investigated in this work.

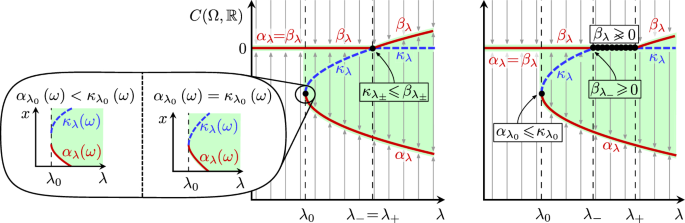
Abstract Image

查看原文本刊更多论文

d -凹非自治标量常微分方程的广义Pitchfork分岔

摘要描述了一个耗散标量非自治常微分方程$$x'=f(t,x)$$ x ' = f (t, x)的两个不同单参数扰动($$+\lambda x$$ + λ x和$$+\lambda x^2$$ + λ x 2)的全局分岔图，假设0是常数解，f在t中循环，其关于x的一阶导数是严格凹函数。斜积形式的使用使我们能够识别最小集数量和全局吸引子形状变化的分岔。在摄动$$+\lambda x$$ + λ x的情况下，可能会出现所谓的广义干草叉分岔，其特点是在自主动力学中缺乏类似物。本文对这种新的分岔模式进行了广泛的研究。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Accounts of Chemical Research 化学-化学综合

CiteScore

31.40

自引率

1.10%

发文量

312

审稿时长

2 months

期刊介绍： Accounts of Chemical Research presents short, concise and critical articles offering easy-to-read overviews of basic research and applications in all areas of chemistry and biochemistry. These short reviews focus on research from the author’s own laboratory and are designed to teach the reader about a research project. In addition, Accounts of Chemical Research publishes commentaries that give an informed opinion on a current research problem. Special Issues online are devoted to a single topic of unusual activity and significance. Accounts of Chemical Research replaces the traditional article abstract with an article "Conspectus." These entries synopsize the research affording the reader a closer look at the content and significance of an article. Through this provision of a more detailed description of the article contents, the Conspectus enhances the article's discoverability by search engines and the exposure for the research.