Low regularity integrators for semilinear parabolic equations with maximum bound principles
IF 1.7
3区 数学
Q3 COMPUTER SCIENCE, SOFTWARE ENGINEERING
引用次数: 1
Abstract
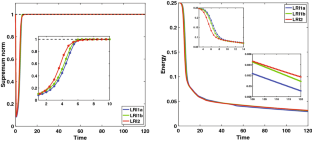
This paper is concerned with conditionally structure-preserving, low regularity time integration methods for a class of semilinear parabolic equations of Allen–Cahn type. Important properties of such equations include maximum bound principle (MBP) and energy dissipation law; for the former, that means the absolute value of the solution is pointwisely bounded for all the time by some constant imposed by appropriate initial and boundary conditions. The model equation is first discretized in space by the central finite difference, then by iteratively using Duhamel’s formula, first- and second-order low regularity integrators (LRIs) are constructed for time discretization of the semi-discrete system. The proposed LRI schemes are proved to preserve the MBP and the energy stability in the discrete sense. Furthermore, their temporal error estimates are also successfully derived under a low regularity requirement that the exact solution of the semi-discrete problem is only assumed to be continuous in time. Numerical results show that the proposed LRI schemes are more accurate and have better convergence rates than classic exponential time differencing schemes, especially when the interfacial parameter approaches zero.
具有最大界原理的半线性抛物方程的低正则积分器
研究了一类半线性抛物型Allen-Cahn方程的条件保结构、低正则性时间积分方法。这类方程的重要性质包括最大界原理和能量耗散规律;对于前者,这意味着解的绝对值始终被适当的初始条件和边界条件所施加的常数点限定。首先利用中心有限差分在空间上离散模型方程,然后利用Duhamel公式迭代构造一阶和二阶低正则积分器对半离散系统进行时间离散。所提出的LRI方案在离散意义上保持了MBP和能量稳定性。此外,在较低的正则性要求下,仅假设半离散问题的精确解在时间上是连续的,也成功地导出了它们的时间误差估计。数值结果表明,与经典的指数时差格式相比,所提出的LRI格式具有更高的精度和更快的收敛速度,特别是当界面参数趋近于零时。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

BIT Numerical Mathematics
数学-计算机:软件工程
CiteScore
2.90
自引率
0.00%
发文量
38
审稿时长
6 months
期刊介绍:
The journal BIT has been published since 1961. BIT publishes original research papers in the rapidly developing field of numerical analysis. The essential areas covered by BIT are development and analysis of numerical methods as well as the design and use of algorithms for scientific computing. Topics emphasized by BIT include numerical methods in approximation, linear algebra, and ordinary and partial differential equations.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


