A Cyclic Constitutive Model Based on Crystal Plasticity for Body-Centered Cubic Cyclic Softening Metals

Abstract

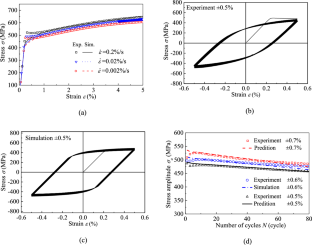
Under the framework of the small deformation crystal plasticity theory, a crystal plastic cyclic constitutive model for body-centered cubic (BCC) cyclic softening polycrystalline metals is established. The constitutive model introduces the isotropic softening rule that includes two different mechanisms: namely softening under monotonic deformation and softening under cyclic deformation on each slip system. Meanwhile, a modified Armstrong-Frederick nonlinear kinematic hardening rule is adopted. The appropriate explicit scale transition rule is selected to extend the single crystal constitutive model to the polycrystalline constitutive model. Then the model is used to predict the uniaxial and multiaxial ratcheting deformation of BCC axle steel EA4T to verify the rationality of the proposed model. The simulation results indicate that the newly established crystal plasticity model can not only describe the cyclic softening characteristics of BCC axle steel EA4T well, but also reasonably describe the evolution laws of uniaxial ratcheting and nonproportional multiaxial ratcheting deformation. Moreover, the established crystal plastic cyclic constitutive model can reasonably predict the ratcheting behavior of BCC single crystal as well.