Temporal to spatial instability in a flow system: a comparison

IF 16.4 1区化学 Q1 CHEMISTRY, MULTIDISCIPLINARY

Accounts of Chemical Research Pub Date : 2023-10-03 DOI:10.1007/s11587-023-00820-x

Antonio Barletta

引用次数: 0

Abstract

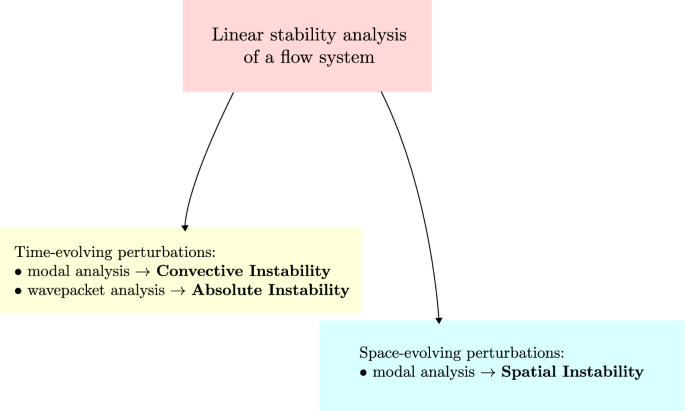
Abstract The definitions of temporal instability and of spatial instability in a flow system are comparatively surveyed. The simple model of one-dimensional Burgers’ flow is taken as the scenario where such different conceptions of instability are described. The temporal analysis of instability stems from Lyapunov’s theory, while the spatial analysis of instability interchanges time and space in defining the evolution variable. Thus, the growth rate parameter for temporally unstable perturbations of a basic flow state is to be replaced by a spatial growth rate when a coordinate assumes the role of evolution variable. Finally, the idea of spatial instability is applied to a Rayleigh-Bénard system given by a fluid-saturated horizontal porous layer with an anisotropic permeability and impermeable boundaries kept at different uniform temperatures.

Abstract Image

查看原文本刊更多论文

流动系统的时空不稳定性:比较

摘要对流动系统中时间不稳定和空间不稳定的定义进行了比较研究。一维Burgers流的简单模型被作为描述这些不同不稳定性概念的场景。不稳定性的时间分析源于李亚普诺夫的理论，而不稳定性的空间分析在定义演化变量时互换了时间和空间。因此，当坐标作为演化变量时，将基本流态的时间不稳定扰动的增长率参数替换为空间增长率。最后，将空间不稳定性的思想应用于具有各向异性渗透率和不渗透边界保持在不同均匀温度的饱和流体水平多孔层所给出的rayleigh - b纳德系统。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Accounts of Chemical Research 化学-化学综合

CiteScore

31.40

自引率

1.10%

发文量

312

审稿时长

2 months

期刊介绍： Accounts of Chemical Research presents short, concise and critical articles offering easy-to-read overviews of basic research and applications in all areas of chemistry and biochemistry. These short reviews focus on research from the author’s own laboratory and are designed to teach the reader about a research project. In addition, Accounts of Chemical Research publishes commentaries that give an informed opinion on a current research problem. Special Issues online are devoted to a single topic of unusual activity and significance. Accounts of Chemical Research replaces the traditional article abstract with an article "Conspectus." These entries synopsize the research affording the reader a closer look at the content and significance of an article. Through this provision of a more detailed description of the article contents, the Conspectus enhances the article's discoverability by search engines and the exposure for the research.