Geometry of prāṇakalāntara in the Lagnaprakaraṇa
IF 0.1
Q4 HISTORY & PHILOSOPHY OF SCIENCE
引用次数: 0
Abstract
The prāṇakalāntara, which is the difference between the longitude of a point on the ecliptic and its corresponding right ascension, is an important parameter in the computation of the lagna (ascendant). Mādhava, in his Lagnaprakaraṇa, proposes six different methods for determining the prāṇakalāntara. Kolachana et al. (Indian J Hist Sci 53(1):1–15, 2018) have discussed these techniques and their underlying rationale in an earlier paper. In this paper, we bring out the geometric significance of these computations, which was not fully elaborated upon in the earlier study. We also show how some of the sophisticated relations can be simply derived using similar triangles.
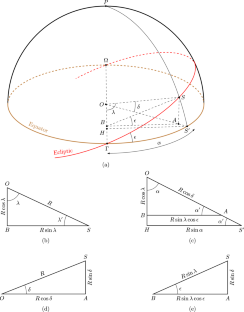
Lagnaprakaraṇa中prāṇakalāntara的几何形状
prāṇakalāntara是黄道上某一点的经度与其对应的赤经之差,是计算上升点的一个重要参数。Mādhava在他的Lagnaprakaraṇa中,提出了六种不同的方法来确定prāṇakalāntara。Kolachana等人(Indian J Hist Sci 53(1):1 - 15,2018)在之前的一篇论文中讨论了这些技术及其基本原理。在本文中,我们提出了这些计算的几何意义,这在早期的研究中没有得到充分的阐述。我们还展示了一些复杂的关系是如何用相似三角形简单地推导出来的。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


