A flexible short recurrence Krylov subspace method for matrices arising in the time integration of port-Hamiltonian systems and ODEs/DAEs with a dissipative Hamiltonian
IF 1.7
3区 数学
Q3 COMPUTER SCIENCE, SOFTWARE ENGINEERING
引用次数: 1
Abstract
Abstract For several classes of mathematical models that yield linear systems, the splitting of the matrix into its Hermitian and skew Hermitian parts is naturally related to properties of the underlying model. This is particularly so for discretizations of dissipative Hamiltonian ODEs, DAEs and port-Hamiltonian systems where, in addition, the Hermitian part is positive definite or semi-definite. It is then possible to develop short recurrence optimal Krylov subspace methods in which the Hermitian part is used as a preconditioner. In this paper, we develop new, right preconditioned variants of this approach which, as their crucial new feature, allow the systems with the Hermitian part to be solved only approximately in each iteration while keeping the short recurrences. This new class of methods is particularly efficient as it allows, for example, to use few steps of a multigrid solver or a (preconditioned) CG method for the Hermitian part in each iteration. We illustrate this with several numerical experiments for large scale systems.
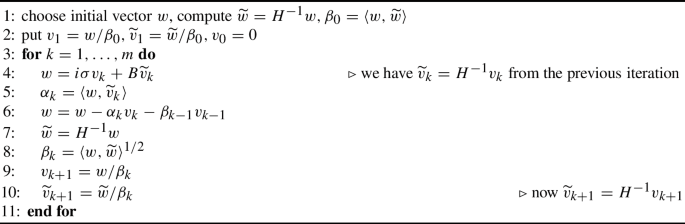
具有耗散哈密顿量的port- hamilton系统和ode /DAEs时间积分中矩阵的柔性短递归Krylov子空间方法
对于几种产生线性系统的数学模型,矩阵分裂为厄米部分和斜厄米部分自然与底层模型的性质有关。对于耗散哈密顿ode, dae和波特哈密顿系统的离散化尤其如此,其中厄米部分是正定或半定的。这样就有可能发展出以厄米部分作为前置条件的短递归最优Krylov子空间方法。在本文中,我们发展了这种方法的新的,正确的预条件的变体,作为其关键的新特征,允许具有厄米部分的系统在每次迭代中只得到近似解,同时保持短递归。这类新方法特别有效,因为它允许,例如,在每次迭代中使用多网格求解器的几个步骤或(预置的)CG方法来处理厄米部分。我们用几个大型系统的数值实验来说明这一点。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

BIT Numerical Mathematics
数学-计算机:软件工程
CiteScore
2.90
自引率
0.00%
发文量
38
审稿时长
6 months
期刊介绍:
The journal BIT has been published since 1961. BIT publishes original research papers in the rapidly developing field of numerical analysis. The essential areas covered by BIT are development and analysis of numerical methods as well as the design and use of algorithms for scientific computing. Topics emphasized by BIT include numerical methods in approximation, linear algebra, and ordinary and partial differential equations.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


