Complexity of limit cycles with block-sequential update schedules in conjunctive networks
IF 1.6
4区 计算机科学
Q3 COMPUTER SCIENCE, ARTIFICIAL INTELLIGENCE
引用次数: 1
Abstract
In this paper, we deal with the following decision problem: given a conjunctive Boolean network defined by its interaction digraph, does it have a limit cycle of a given length k? We prove that this problem is NP-complete in general if k is a parameter of the problem and is in P if the interaction digraph is strongly connected. The case where k is fixed, but the interaction digraph is not strongly connected, remains open. Furthermore, we study some variations of the decision problem: given a conjunctive Boolean network, does there exist a block-sequential (resp. sequential) update schedule such that there is a limit cycle of length k? We prove that these problems are NP-complete for any fixed constant $$k \ge 2$$ .
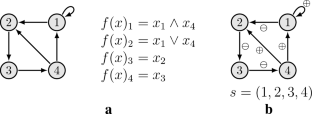
联合网络中具有块顺序更新调度的极限环的复杂性
在本文中,我们处理以下决策问题:给定一个由其交互有向图定义的合布尔网络,它是否具有给定长度k的极限环?我们证明了如果k是问题的一个参数,那么这个问题一般是np完全的,如果相互作用有向图是强连通的,那么这个问题在P内。k是固定的,但是相互作用有向图不是强连接的情况,仍然是开放的。此外,我们还研究了决策问题的一些变体:给定一个合布尔网络,是否存在一个块顺序网络?序列更新计划使得存在长度为k?我们证明了这些问题对于任意固定常数$$k \ge 2$$都是np完全的。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Natural Computing
Computer Science-Computer Science Applications
CiteScore
4.40
自引率
4.80%
发文量
49
审稿时长
3 months
期刊介绍:
The journal is soliciting papers on all aspects of natural computing. Because of the interdisciplinary character of the journal a special effort will be made to solicit survey, review, and tutorial papers which would make research trends in a given subarea more accessible to the broad audience of the journal.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


