一种基于超高维特征的无超参数、快速高效的有限样本聚类检测框架
IF 3.6
3区 计算机科学
Q2 COMPUTER SCIENCE, INFORMATION SYSTEMS
引用次数: 0
摘要
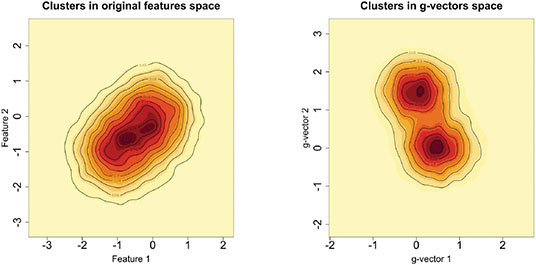
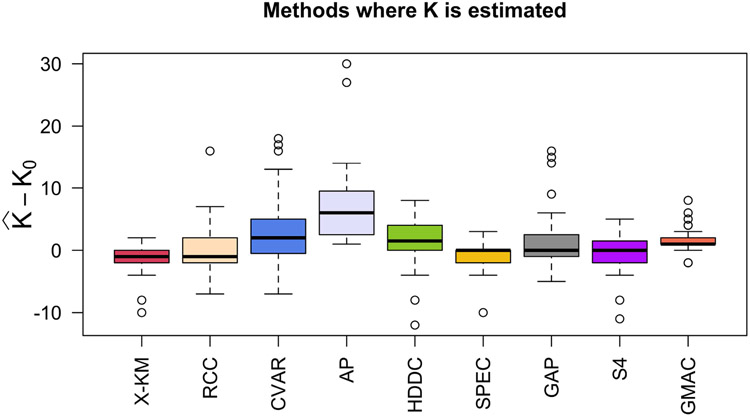
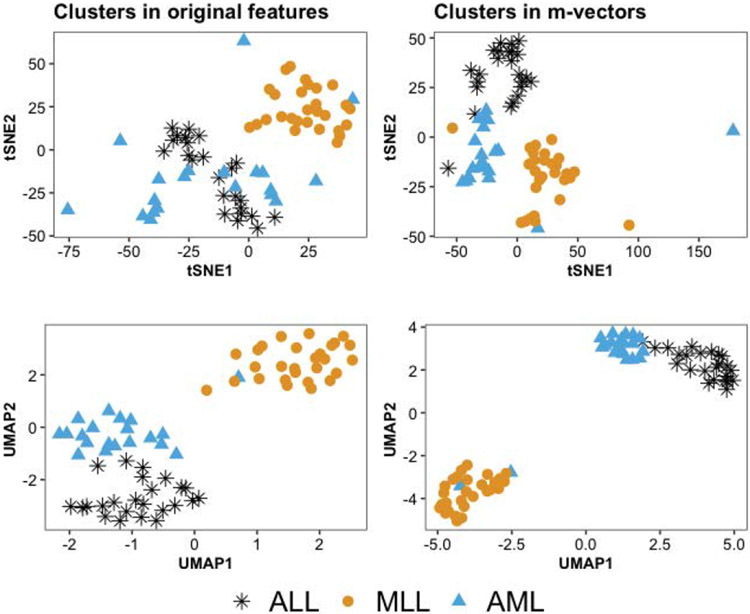
聚类是机器学习中一个具有挑战性的问题,在机器学习中,人们试图根据每个对象上测量的$P$特征将$N$对象分组为$K_{0}$组。在本文中,我们研究了$N\ll P$和$K_{0}$未知的情况。在这种高维、小样本的环境中进行聚类在生物学、医学、社会科学、临床试验以及其他科学和实验领域有许多应用。尽管大多数现有的聚类算法要么需要先验地知道聚类的数量,要么对调整参数的选择敏感,但我们的方法不需要$K_{0}$的先验规范或任何调整参数。这代表了我们方法的一个重要优势,因为训练数据在我们考虑的应用程序中(即在无监督学习问题中)是不可用的。如果没有训练数据,估计$K_{0}$和其他超参数——从而应用替代聚类算法——可能会很困难,并导致不准确的结果。我们的方法是基于Gram矩阵的一个简单变换和强数定律对变换矩阵的应用。如果特征之间的相关性随着特征数量的增长而衰减,我们表明,在低维空间中,变换后的特征向量紧紧围绕着它们各自的聚类期望。这一结果简化了未知集群配置的检测和可视化。我们通过将该算法应用于32个基准微阵列数据集来说明该算法,每个数据集包含在相对较少的组织样本上测量的数千个基因组特征。与其他21种常用的聚类方法相比,我们发现所提出的算法在确定“最佳”聚类配置方面更快,准确率是其他方法的两倍。本文章由计算机程序翻译,如有差异,请以英文原文为准。
A Hyperparameter-Free, Fast and Efficient Framework to Detect Clusters From Limited Samples Based on Ultra High-Dimensional Features
Clustering is a challenging problem in machine learning in which one attempts to group
$N$
objects into
$K_{0}$
groups based on
$P$
features measured on each object. In this article, we examine the case where
$N \ll P$
and
$K_{0}$
is not known. Clustering in such high dimensional, small sample size settings has numerous applications in biology, medicine, the social sciences, clinical trials, and other scientific and experimental fields. Whereas most existing clustering algorithms either require the number of clusters to be known a priori or are sensitive to the choice of tuning parameters, our method does not require the prior specification of
$K_{0}$
or any tuning parameters. This represents an important advantage for our method because training data are not available in the applications we consider (i.e., in unsupervised learning problems). Without training data, estimating
$K_{0}$
and other hyperparameters–and thus applying alternative clustering algorithms–can be difficult and lead to inaccurate results. Our method is based on a simple transformation of the Gram matrix and application of the strong law of large numbers to the transformed matrix. If the correlation between features decays as the number of features grows, we show that the transformed feature vectors concentrate tightly around their respective cluster expectations in a low-dimensional space. This result simplifies the detection and visualization of the unknown cluster configuration. We illustrate the algorithm by applying it to 32 benchmarked microarray datasets, each containing thousands of genomic features measured on a relatively small number of tissue samples. Compared to 21 other commonly used clustering methods, we find that the proposed algorithm is faster and twice as accurate in determining the “best” cluster configuration.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

IEEE Access
COMPUTER SCIENCE, INFORMATION SYSTEMSENGIN-ENGINEERING, ELECTRICAL & ELECTRONIC
CiteScore
9.80
自引率
7.70%
发文量
6673
审稿时长
6 weeks
期刊介绍:
IEEE Access® is a multidisciplinary, open access (OA), applications-oriented, all-electronic archival journal that continuously presents the results of original research or development across all of IEEE''s fields of interest.
IEEE Access will publish articles that are of high interest to readers, original, technically correct, and clearly presented. Supported by author publication charges (APC), its hallmarks are a rapid peer review and publication process with open access to all readers. Unlike IEEE''s traditional Transactions or Journals, reviews are "binary", in that reviewers will either Accept or Reject an article in the form it is submitted in order to achieve rapid turnaround. Especially encouraged are submissions on:
Multidisciplinary topics, or applications-oriented articles and negative results that do not fit within the scope of IEEE''s traditional journals.
Practical articles discussing new experiments or measurement techniques, interesting solutions to engineering.
Development of new or improved fabrication or manufacturing techniques.
Reviews or survey articles of new or evolving fields oriented to assist others in understanding the new area.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


