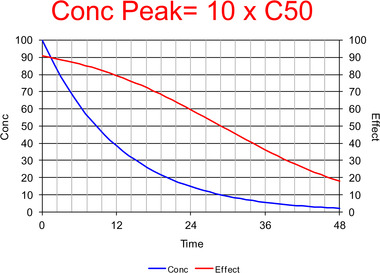
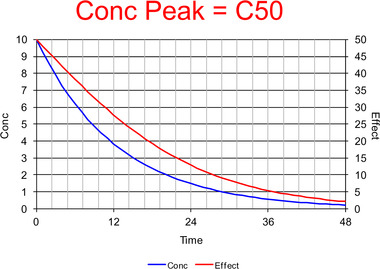
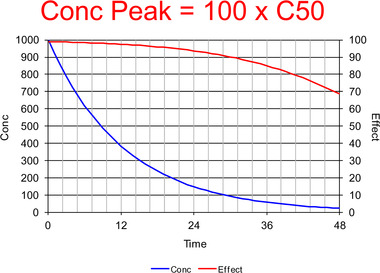
Commentary on Pharmacologically Meaningful Half-Life.

Chaiken and Pai have proposed that there is a need for a pharmacologically meaningful half-life in order to provide a single descriptor to account for the duration of pharmacologic effect and dosing interval.1 Although they show in their introductory remarks that they are aware of pharmacometrics and systems biology, they have also clearly illustrated the limitations of a single parameter to describe the relationship between concentration and effect. A description of the time course of drug effect, and hence the duration, requires, at a minimum, a description of the time course of concentration and the relationship between concentration and effect. The simplest pharmacokinetic model for the time course of concentration involves a bolus input, a single distribution volume (V), and a first-order elimination process, defined by clearance (CL). The simplest realistic pharmacodynamic model has a maximum effect (Emax) and the concentration at 50% of Emax (C50). Ignoring more realistic input processes and delays between plasma concentration and effect, this means that a minimum of four parameters are required (V, CL, Emax, and C50). Thus, even the simplest description that can account for the duration of pharmacologic effect requires four parameters it is logically impossible and scientifically incorrect to imagine that a single half-life parameter can be found to describe the complexity. This is illustrated in Figures 1–3, which show the dramatic change in the duration of drug effect with increasing initial concentration (equivalent to increasing dose). The pharmacokinetic and pharmacodynamic parameters rest unchanged only the dose has changed. There is no single half-life that can predict or explain these changes based on the simplest possible realistic description of drug effect. Instead of searching for the impossible by looking for a single half-life to describe complex drug effects, clinicians are advised to learn the basic principles Figure 1. Time course of concentration (blue) and effect (red) with a peak concentration equal to C50. The concentration half-life is about 7 time units. Concentrations are mainly lower than the C50, and thus the effect is approximately proportional to the concentration. The time course of the effect is similar to the time course of concentration, but does not follow the exponential decrease and therefore cannot be described with a half-life of effect.