用最小加代数求解高维最优控制问题和Hamilton-Jacobi偏微分方程的神经网络结构

IF 1.8 4区计算机科学 Q3 AUTOMATION & CONTROL SYSTEMS

Mathematics of Control Signals and Systems Pub Date : 2021-05-07 DOI:10.1007/s00498-022-00333-2

J. Darbon, P. Dower, Tingwei Meng

引用次数: 11

摘要

本文章由计算机程序翻译，如有差异，请以英文原文为准。

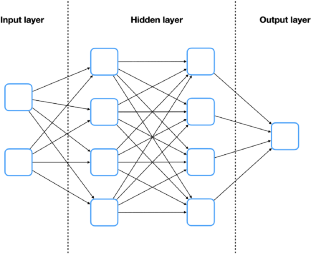
Neural network architectures using min-plus algebra for solving certain high-dimensional optimal control problems and Hamilton–Jacobi PDEs

查看原文本刊更多论文

Neural network architectures using min-plus algebra for solving certain high-dimensional optimal control problems and Hamilton–Jacobi PDEs

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Mathematics of Control Signals and Systems 工程技术-工程：电子与电气

CiteScore

2.90

自引率

0.00%

发文量

审稿时长

>12 weeks

期刊介绍： Mathematics of Control, Signals, and Systems (MCSS) is an international journal devoted to mathematical control and system theory, including system theoretic aspects of signal processing. Its unique feature is its focus on mathematical system theory; it concentrates on the mathematical theory of systems with inputs and/or outputs and dynamics that are typically described by deterministic or stochastic ordinary or partial differential equations, differential algebraic equations or difference equations. Potential topics include, but are not limited to controllability, observability, and realization theory, stability theory of nonlinear systems, system identification, mathematical aspects of switched, hybrid, networked, and stochastic systems, and system theoretic aspects of optimal control and other controller design techniques. Application oriented papers are welcome if they contain a significant theoretical contribution.