一种改进的二次插值寻根方法

IF 0.58 Q3 Engineering

Journal of Applied and Industrial Mathematics Pub Date : 2023-11-04 DOI:10.1134/S1990478923030031

V. V. Bogdanov, Yu. S. Volkov

{"title":"一种改进的二次插值寻根方法","authors":"V. V. Bogdanov, Yu. S. Volkov","doi":"10.1134/S1990478923030031","DOIUrl":null,"url":null,"abstract":"<p> A modification of the quadratic interpolation method for finding the root of a continuous\nfunction is proposed. Two quadratic interpolation polynomials are simultaneously constructed. It\nis shown that if the third derivative of the original function does not change sign on the considered\ninterval of localization of the required root, then the root lies between the roots of the quadratic\nfunctions. This allows one to substantially narrow the localization interval and reduce the number\nof steps to calculate the root with a given accuracy. The proposed modification of the quadratic\ninterpolation method is used in the problem of calculating isolines when modeling the hill diagram\nof hydraulic turbines.\n</p>","PeriodicalId":607,"journal":{"name":"Journal of Applied and Industrial Mathematics","volume":"17 3","pages":"491 - 497"},"PeriodicalIF":0.5800,"publicationDate":"2023-11-04","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"A Modified Quadratic Interpolation Method for Root Finding\",\"authors\":\"V. V. Bogdanov, Yu. S. Volkov\",\"doi\":\"10.1134/S1990478923030031\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p> A modification of the quadratic interpolation method for finding the root of a continuous\\nfunction is proposed. Two quadratic interpolation polynomials are simultaneously constructed. It\\nis shown that if the third derivative of the original function does not change sign on the considered\\ninterval of localization of the required root, then the root lies between the roots of the quadratic\\nfunctions. This allows one to substantially narrow the localization interval and reduce the number\\nof steps to calculate the root with a given accuracy. The proposed modification of the quadratic\\ninterpolation method is used in the problem of calculating isolines when modeling the hill diagram\\nof hydraulic turbines.\\n</p>\",\"PeriodicalId\":607,\"journal\":{\"name\":\"Journal of Applied and Industrial Mathematics\",\"volume\":\"17 3\",\"pages\":\"491 - 497\"},\"PeriodicalIF\":0.5800,\"publicationDate\":\"2023-11-04\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Applied and Industrial Mathematics\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://link.springer.com/article/10.1134/S1990478923030031\",\"RegionNum\":0,\"RegionCategory\":null,\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"Engineering\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Applied and Industrial Mathematics","FirstCategoryId":"1085","ListUrlMain":"https://link.springer.com/article/10.1134/S1990478923030031","RegionNum":0,"RegionCategory":null,"ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"Engineering","Score":null,"Total":0}

引用次数: 0

摘要

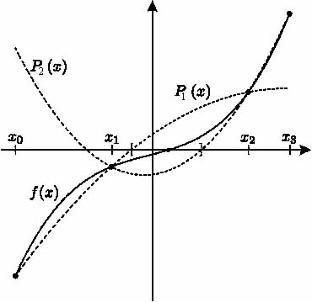
对求连续函数根的二次插值方法进行了改进。同时构造了两个二次插值多项式。结果表明，如果原函数的三阶导数在所需根的考虑定位区间上不改变符号，则根位于二次函数的根之间。这允许人们实质上缩小定位间隔，并减少以给定精度计算根的步骤数量。将二次插值法的改进应用于水轮机山形图建模时等值线的计算问题。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

A Modified Quadratic Interpolation Method for Root Finding

查看原文本刊更多论文

A Modified Quadratic Interpolation Method for Root Finding

A modification of the quadratic interpolation method for finding the root of a continuous function is proposed. Two quadratic interpolation polynomials are simultaneously constructed. It is shown that if the third derivative of the original function does not change sign on the considered interval of localization of the required root, then the root lies between the roots of the quadratic functions. This allows one to substantially narrow the localization interval and reduce the number of steps to calculate the root with a given accuracy. The proposed modification of the quadratic interpolation method is used in the problem of calculating isolines when modeling the hill diagram of hydraulic turbines.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Applied and Industrial Mathematics Engineering-Industrial and Manufacturing Engineering

CiteScore

1.00

自引率

0.00%

发文量

期刊介绍： Journal of Applied and Industrial Mathematics is a journal that publishes original and review articles containing theoretical results and those of interest for applications in various branches of industry. The journal topics include the qualitative theory of differential equations in application to mechanics, physics, chemistry, biology, technical and natural processes; mathematical modeling in mechanics, physics, engineering, chemistry, biology, ecology, medicine, etc.; control theory; discrete optimization; discrete structures and extremum problems; combinatorics; control and reliability of discrete circuits; mathematical programming; mathematical models and methods for making optimal decisions; models of theory of scheduling, location and replacement of equipment; modeling the control processes; development and analysis of algorithms; synthesis and complexity of control systems; automata theory; graph theory; game theory and its applications; coding theory; scheduling theory; and theory of circuits.