关于具有给定直径和距离-（k）无关集极值的树

IF 0.58 Q3 Engineering

Journal of Applied and Industrial Mathematics Pub Date : 2023-11-04 DOI:10.1134/S1990478923030195

D. S. Taletskii

{"title":"关于具有给定直径和距离-（k）无关集极值的树","authors":"D. S. Taletskii","doi":"10.1134/S1990478923030195","DOIUrl":null,"url":null,"abstract":" The set of vertices of a graph is called distance-\n\$ k \$ independent if the distance between\nany two of its vertices is greater than some integer\n\$ k \\geq 1 \$. In this paper, we describe\n\$ n \$-vertex trees with a given diameter\n\$ d \$ that have the maximum and minimum possible number of distance-\n\$ k \$ independent sets among all such trees. The maximum problem is solvable for\nthe case of\n\$ 1 < k < d \\leq 5 \$. The minimum problem is much simpler and can be solved for all\n\$ 1 < k < d < n \$. \n","PeriodicalId":607,"journal":{"name":"Journal of Applied and Industrial Mathematics","volume":"17 3","pages":"664 - 677"},"PeriodicalIF":0.5800,"publicationDate":"2023-11-04","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"On Trees with a Given Diameter and the Extremal Number of Distance-\\\$k\\\$ Independent Sets\",\"authors\":\"D. S. Taletskii\",\"doi\":\"10.1134/S1990478923030195\",\"DOIUrl\":null,\"url\":null,\"abstract\":\" The set of vertices of a graph is called distance-\\n\\\$ k \\\$ independent if the distance between\\nany two of its vertices is greater than some integer\\n\\\$ k \\\\geq 1 \\\$. In this paper, we describe\\n\\\$ n \\\$-vertex trees with a given diameter\\n\\\$ d \\\$ that have the maximum and minimum possible number of distance-\\n\\\$ k \\\$ independent sets among all such trees. The maximum problem is solvable for\\nthe case of\\n\\\$ 1 < k < d \\\\leq 5 \\\$. The minimum problem is much simpler and can be solved for all\\n\\\$ 1 < k < d < n \\\$. \\n\",\"PeriodicalId\":607,\"journal\":{\"name\":\"Journal of Applied and Industrial Mathematics\",\"volume\":\"17 3\",\"pages\":\"664 - 677\"},\"PeriodicalIF\":0.5800,\"publicationDate\":\"2023-11-04\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Applied and Industrial Mathematics\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://link.springer.com/article/10.1134/S1990478923030195\",\"RegionNum\":0,\"RegionCategory\":null,\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"Engineering\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Applied and Industrial Mathematics","FirstCategoryId":"1085","ListUrlMain":"https://link.springer.com/article/10.1134/S1990478923030195","RegionNum":0,"RegionCategory":null,"ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"Engineering","Score":null,"Total":0}

引用次数: 0

摘要

如果图的任意两个顶点之间的距离大于某个整数（k\geq1\），则图的顶点集称为距离-（k\）无关。在本文中，我们描述了具有给定直径的顶点树，这些树在所有这些树中具有最大和最小可能的距离无关集。最大问题对于\（1<；k<；d\leq 5\）的情况是可解的。最小问题要简单得多，并且可以为所有的\（1<；k<；d<；n\）求解。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

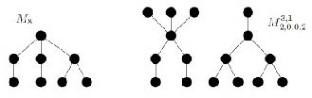
$On Trees with a Given Diameter and the Extremal Number of Distance-$k$ Independent Sets$

查看原文本刊更多论文

On Trees with a Given Diameter and the Extremal Number of Distance-$k$ Independent Sets

The set of vertices of a graph is called distance- $ k $ independent if the distance between any two of its vertices is greater than some integer $ k \geq 1 $. In this paper, we describe $ n $-vertex trees with a given diameter $ d $ that have the maximum and minimum possible number of distance- $ k $ independent sets among all such trees. The maximum problem is solvable for the case of $ 1 < k < d \leq 5 $. The minimum problem is much simpler and can be solved for all $ 1 < k < d < n $.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Applied and Industrial Mathematics Engineering-Industrial and Manufacturing Engineering

CiteScore

1.00

自引率

0.00%

发文量

期刊介绍： Journal of Applied and Industrial Mathematics is a journal that publishes original and review articles containing theoretical results and those of interest for applications in various branches of industry. The journal topics include the qualitative theory of differential equations in application to mechanics, physics, chemistry, biology, technical and natural processes; mathematical modeling in mechanics, physics, engineering, chemistry, biology, ecology, medicine, etc.; control theory; discrete optimization; discrete structures and extremum problems; combinatorics; control and reliability of discrete circuits; mathematical programming; mathematical models and methods for making optimal decisions; models of theory of scheduling, location and replacement of equipment; modeling the control processes; development and analysis of algorithms; synthesis and complexity of control systems; automata theory; graph theory; game theory and its applications; coding theory; scheduling theory; and theory of circuits.