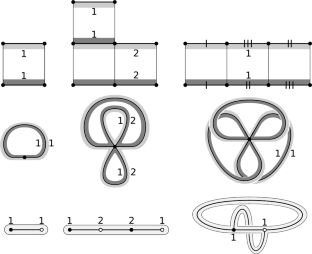
Contribution of n-cylinder square-tiled surfaces to Masur–Veech volume of $\mathcal{H}(2g-2)$

We find the generating function for the contributions of n-cylinder square-tiled surfaces to the Masur–Veech volume of \(\mathcal{H}(2g-2)\). It is a bivariate generalization of the generating function for the total volumes obtained by Sauvaget via intersection theory. Our approach is, however, purely combinatorial. It relies on the study of counting functions for certain families of metric ribbon graphs. Their top-degree terms are polynomials, whose (normalized) coefficients are cardinalities of certain families of metric plane trees. These polynomials are analogues of Kontsevich polynomials that appear as part of his proof of Witten’s conjecture.