增加一个实数后，测量结果趋于一致。

IF 0.3 4区数学 Q1 Arts and Humanities

Archive for Mathematical Logic Pub Date : 2023-08-11 DOI:10.1007/s00153-023-00888-0

Damian Sobota, Lyubomyr Zdomskyy

{"title":"增加一个实数后，测量结果趋于一致。","authors":"Damian Sobota, Lyubomyr Zdomskyy","doi":"10.1007/s00153-023-00888-0","DOIUrl":null,"url":null,"abstract":"<div>We prove that if \\(\\mathcal {A}\\) is an infinite Boolean algebra in the ground model V and \\(\\mathbb {P}\\) is a notion of forcing adding any of the following reals: a Cohen real, an unsplit real, or a random real, then, in any \\(\\mathbb {P}\\)-generic extension V[G], \\(\\mathcal {A}\\) has neither the Nikodym property nor the Grothendieck property. A similar result is also proved for a dominating real and the Nikodym property.</div>","PeriodicalId":48853,"journal":{"name":"Archive for Mathematical Logic","volume":null,"pages":null},"PeriodicalIF":0.3000,"publicationDate":"2023-08-11","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC10787011/pdf/","citationCount":"0","resultStr":"{\"title\":\"Convergence of measures after adding a real\",\"authors\":\"Damian Sobota, Lyubomyr Zdomskyy\",\"doi\":\"10.1007/s00153-023-00888-0\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div>We prove that if \\\\(\\\\mathcal {A}\\\\) is an infinite Boolean algebra in the ground model V and \\\\(\\\\mathbb {P}\\\\) is a notion of forcing adding any of the following reals: a Cohen real, an unsplit real, or a random real, then, in any \\\\(\\\\mathbb {P}\\\\)-generic extension V[G], \\\\(\\\\mathcal {A}\\\\) has neither the Nikodym property nor the Grothendieck property. A similar result is also proved for a dominating real and the Nikodym property.</div>\",\"PeriodicalId\":48853,\"journal\":{\"name\":\"Archive for Mathematical Logic\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.3000,\"publicationDate\":\"2023-08-11\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://www.ncbi.nlm.nih.gov/pmc/articles/PMC10787011/pdf/\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Archive for Mathematical Logic\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s00153-023-00888-0\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"Arts and Humanities\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Archive for Mathematical Logic","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s00153-023-00888-0","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"Arts and Humanities","Score":null,"Total":0}

引用次数: 0

摘要

我们证明，如果 A 是基础模型 V 中的一个无穷布尔代数，而 P 是一个强制添加以下任何一个实数的概念：一个科恩实数、一个未分割实数或一个随机实数，那么在任何 P 代扩展 V[G] 中，A 既不具有尼科德姆性质，也不具有格罗thendieck 性质。对于支配实数和尼科戴姆性质，也证明了类似的结果。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

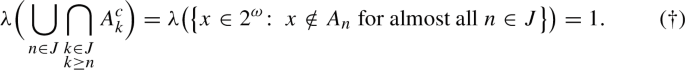
Convergence of measures after adding a real

查看原文本刊更多论文

Convergence of measures after adding a real

We prove that if \(\mathcal {A}\) is an infinite Boolean algebra in the ground model V and \(\mathbb {P}\) is a notion of forcing adding any of the following reals: a Cohen real, an unsplit real, or a random real, then, in any \(\mathbb {P}\)-generic extension V[G], \(\mathcal {A}\) has neither the Nikodym property nor the Grothendieck property. A similar result is also proved for a dominating real and the Nikodym property.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Archive for Mathematical Logic MATHEMATICS-LOGIC

CiteScore

0.80

自引率

0.00%

发文量

审稿时长

6-12 weeks

期刊介绍： The journal publishes research papers and occasionally surveys or expositions on mathematical logic. Contributions are also welcomed from other related areas, such as theoretical computer science or philosophy, as long as the methods of mathematical logic play a significant role. The journal therefore addresses logicians and mathematicians, computer scientists, and philosophers who are interested in the applications of mathematical logic in their own field, as well as its interactions with other areas of research.