具有初始应力效应的温克勒-帕斯捷尔纳克地基中功能梯度纳米板的波传播

IF 1.8 4区材料科学 Q2 MATERIALS SCIENCE, CHARACTERIZATION & TESTING

Physical Mesomechanics Pub Date : 2023-06-30 DOI:10.1134/S1029959923030049

M. Ellali, M. Bouazza, A. M. Zenkour

{"title":"具有初始应力效应的温克勒-帕斯捷尔纳克地基中功能梯度纳米板的波传播","authors":"M. Ellali, M. Bouazza, A. M. Zenkour","doi":"10.1134/S1029959923030049","DOIUrl":null,"url":null,"abstract":"<p>This paper presents the analysis of wave propagation in functionally-graded (FG) nanoplates on a Winkler–Pasternak foundation. The investigation is carried out in the framework of nonlocal elasticity theory and a new four-unknown higher-order displacement theory including indeterminate integral terms. Hamilton’s principle and Navier’s method are used to obtain the frequency relations of FG nanoplates for different conditions by solving an eigenvalue problem. The obtained results for the frequency and phase velocity of wave propagation in an FG nanoplate are compared with recent outcomes of similar research.</p>","PeriodicalId":726,"journal":{"name":"Physical Mesomechanics","volume":null,"pages":null},"PeriodicalIF":1.8000,"publicationDate":"2023-06-30","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Wave Propagation in Functionally-Graded Nanoplates Embedded in a Winkler–Pasternak Foundation with Initial Stress Effect\",\"authors\":\"M. Ellali, M. Bouazza, A. M. Zenkour\",\"doi\":\"10.1134/S1029959923030049\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>This paper presents the analysis of wave propagation in functionally-graded (FG) nanoplates on a Winkler–Pasternak foundation. The investigation is carried out in the framework of nonlocal elasticity theory and a new four-unknown higher-order displacement theory including indeterminate integral terms. Hamilton’s principle and Navier’s method are used to obtain the frequency relations of FG nanoplates for different conditions by solving an eigenvalue problem. The obtained results for the frequency and phase velocity of wave propagation in an FG nanoplate are compared with recent outcomes of similar research.</p>\",\"PeriodicalId\":726,\"journal\":{\"name\":\"Physical Mesomechanics\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":1.8000,\"publicationDate\":\"2023-06-30\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Physical Mesomechanics\",\"FirstCategoryId\":\"88\",\"ListUrlMain\":\"https://link.springer.com/article/10.1134/S1029959923030049\",\"RegionNum\":4,\"RegionCategory\":\"材料科学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MATERIALS SCIENCE, CHARACTERIZATION & TESTING\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Physical Mesomechanics","FirstCategoryId":"88","ListUrlMain":"https://link.springer.com/article/10.1134/S1029959923030049","RegionNum":4,"RegionCategory":"材料科学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATERIALS SCIENCE, CHARACTERIZATION & TESTING","Score":null,"Total":0}

引用次数: 0

摘要

本文对温克勒-帕斯捷尔纳克地基上功能梯度纳米片中的波传播特性进行了分析。在非局部弹性理论和包含不定积分项的四未知高阶位移理论的框架下进行了研究。利用Hamilton原理和Navier方法求解特征值问题，得到了不同条件下FG纳米片的频率关系。所得的波在FG纳米片中的传播频率和相速度的结果与最近的类似研究结果进行了比较。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

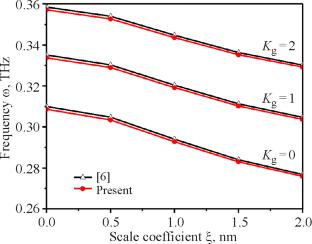
Wave Propagation in Functionally-Graded Nanoplates Embedded in a Winkler–Pasternak Foundation with Initial Stress Effect

查看原文本刊更多论文

Wave Propagation in Functionally-Graded Nanoplates Embedded in a Winkler–Pasternak Foundation with Initial Stress Effect

This paper presents the analysis of wave propagation in functionally-graded (FG) nanoplates on a Winkler–Pasternak foundation. The investigation is carried out in the framework of nonlocal elasticity theory and a new four-unknown higher-order displacement theory including indeterminate integral terms. Hamilton’s principle and Navier’s method are used to obtain the frequency relations of FG nanoplates for different conditions by solving an eigenvalue problem. The obtained results for the frequency and phase velocity of wave propagation in an FG nanoplate are compared with recent outcomes of similar research.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Physical Mesomechanics Materials Science-General Materials Science

CiteScore

3.50

自引率

18.80%

发文量

期刊介绍： The journal provides an international medium for the publication of theoretical and experimental studies and reviews related in the physical mesomechanics and also solid-state physics, mechanics, materials science, geodynamics, non-destructive testing and in a large number of other fields where the physical mesomechanics may be used extensively. Papers dealing with the processing, characterization, structure and physical properties and computational aspects of the mesomechanics of heterogeneous media, fracture mesomechanics, physical mesomechanics of materials, mesomechanics applications for geodynamics and tectonics, mesomechanics of smart materials and materials for electronics, non-destructive testing are viewed as suitable for publication.