三角剖分中三角元退化估计的一种方法

IF 0.5 4区数学 Q3 MATHEMATICS

Doklady Mathematics Pub Date : 2023-08-30 DOI:10.1134/S106456242370076X

Yu. A. Kriksin, V. F. Tishkin

{"title":"三角剖分中三角元退化估计的一种方法","authors":"Yu. A. Kriksin,  V. F. Tishkin","doi":"10.1134/S106456242370076X","DOIUrl":null,"url":null,"abstract":"<p>A quantitative estimate for the quality of a triangular element—the triangle degeneration index—is proposed. To apply this estimate, a simple model triangulation is constructed in which the vertex coordinates are obtained as the sum of the corresponding node coordinates in a given regular grid and their random increments. For various parameter values, the empirical distribution function of the triangle degeneration index is calculated, which is considered a quantitative characteristic of the quality of triangular elements in the constructed triangulation.</p>","PeriodicalId":531,"journal":{"name":"Doklady Mathematics","volume":"107 2","pages":"126 - 129"},"PeriodicalIF":0.5000,"publicationDate":"2023-08-30","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"On One Approach to the Estimation of a Triangular Element Degeneration in a Triangulation\",\"authors\":\"Yu. A. Kriksin,  V. F. Tishkin\",\"doi\":\"10.1134/S106456242370076X\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>A quantitative estimate for the quality of a triangular element—the triangle degeneration index—is proposed. To apply this estimate, a simple model triangulation is constructed in which the vertex coordinates are obtained as the sum of the corresponding node coordinates in a given regular grid and their random increments. For various parameter values, the empirical distribution function of the triangle degeneration index is calculated, which is considered a quantitative characteristic of the quality of triangular elements in the constructed triangulation.</p>\",\"PeriodicalId\":531,\"journal\":{\"name\":\"Doklady Mathematics\",\"volume\":\"107 2\",\"pages\":\"126 - 129\"},\"PeriodicalIF\":0.5000,\"publicationDate\":\"2023-08-30\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Doklady Mathematics\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1134/S106456242370076X\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Doklady Mathematics","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1134/S106456242370076X","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

提出了三角元质量的一种定量估计方法——三角退化指数。为了应用这个估计，构造了一个简单的模型三角剖分，其中顶点坐标是给定规则网格中相应节点坐标及其随机增量的和。对于不同的参数值，计算三角退化指数的经验分布函数，认为这是构造三角网中三角单元质量的定量特征。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

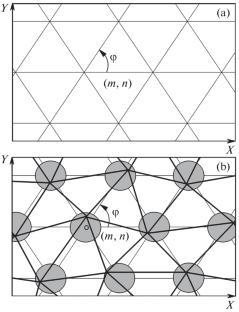
On One Approach to the Estimation of a Triangular Element Degeneration in a Triangulation

查看原文本刊更多论文

On One Approach to the Estimation of a Triangular Element Degeneration in a Triangulation

A quantitative estimate for the quality of a triangular element—the triangle degeneration index—is proposed. To apply this estimate, a simple model triangulation is constructed in which the vertex coordinates are obtained as the sum of the corresponding node coordinates in a given regular grid and their random increments. For various parameter values, the empirical distribution function of the triangle degeneration index is calculated, which is considered a quantitative characteristic of the quality of triangular elements in the constructed triangulation.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Doklady Mathematics 数学-数学

CiteScore

1.00

自引率

16.70%

发文量

审稿时长

3-6 weeks

期刊介绍： Doklady Mathematics is a journal of the Presidium of the Russian Academy of Sciences. It contains English translations of papers published in Doklady Akademii Nauk (Proceedings of the Russian Academy of Sciences), which was founded in 1933 and is published 36 times a year. Doklady Mathematics includes the materials from the following areas: mathematics, mathematical physics, computer science, control theory, and computers. It publishes brief scientific reports on previously unpublished significant new research in mathematics and its applications. The main contributors to the journal are Members of the RAS, Corresponding Members of the RAS, and scientists from the former Soviet Union and other foreign countries. Among the contributors are the outstanding Russian mathematicians.