非交换霍奇理论中的公式

IF 0.5 4区数学

Journal of Homotopy and Related Structures Pub Date : 2019-11-21 DOI:10.1007/s40062-019-00251-2

Nick Sheridan

{"title":"非交换霍奇理论中的公式","authors":"Nick Sheridan","doi":"10.1007/s40062-019-00251-2","DOIUrl":null,"url":null,"abstract":"We prove that the cyclic homology of a saturated \\(A_\\infty \\) category admits the structure of a ‘polarized variation of Hodge structures’, building heavily on the work of many authors: the main point of the paper is to present complete proofs, and also explicit formulae for all of the relevant structures. This forms part of a project of Ganatra, Perutz and the author, to prove that homological mirror symmetry implies enumerative mirror symmetry.","PeriodicalId":636,"journal":{"name":"Journal of Homotopy and Related Structures","volume":"15 1","pages":"249 - 299"},"PeriodicalIF":0.5000,"publicationDate":"2019-11-21","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://sci-hub-pdf.com/10.1007/s40062-019-00251-2","citationCount":"33","resultStr":"{\"title\":\"Formulae in noncommutative Hodge theory\",\"authors\":\"Nick Sheridan\",\"doi\":\"10.1007/s40062-019-00251-2\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"We prove that the cyclic homology of a saturated \\\\(A_\\\\infty \\\\) category admits the structure of a ‘polarized variation of Hodge structures’, building heavily on the work of many authors: the main point of the paper is to present complete proofs, and also explicit formulae for all of the relevant structures. This forms part of a project of Ganatra, Perutz and the author, to prove that homological mirror symmetry implies enumerative mirror symmetry.\",\"PeriodicalId\":636,\"journal\":{\"name\":\"Journal of Homotopy and Related Structures\",\"volume\":\"15 1\",\"pages\":\"249 - 299\"},\"PeriodicalIF\":0.5000,\"publicationDate\":\"2019-11-21\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://sci-hub-pdf.com/10.1007/s40062-019-00251-2\",\"citationCount\":\"33\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Homotopy and Related Structures\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s40062-019-00251-2\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"\",\"JCRName\":\"\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Homotopy and Related Structures","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s40062-019-00251-2","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"","JCRName":"","Score":null,"Total":0}

引用次数: 33

摘要

我们证明了饱和\(A_\infty \)范畴的循环同调承认“Hodge结构的极化变异”的结构，这在很大程度上是建立在许多作者的工作基础上的:本文的重点是给出完整的证明，以及所有相关结构的显式公式。这构成了Ganatra, Perutz和作者的一个项目的一部分，以证明同调镜像对称意味着枚举镜像对称。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

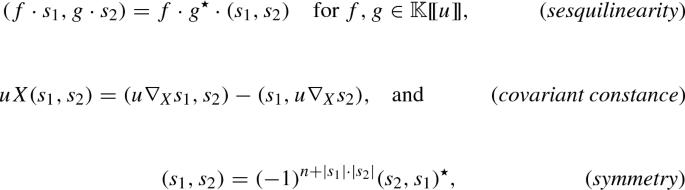
Formulae in noncommutative Hodge theory

查看原文本刊更多论文

Formulae in noncommutative Hodge theory

We prove that the cyclic homology of a saturated \(A_\infty \) category admits the structure of a ‘polarized variation of Hodge structures’, building heavily on the work of many authors: the main point of the paper is to present complete proofs, and also explicit formulae for all of the relevant structures. This forms part of a project of Ganatra, Perutz and the author, to prove that homological mirror symmetry implies enumerative mirror symmetry.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Homotopy and Related Structures Mathematics-Geometry and Topology

自引率

0.00%

发文量

期刊介绍： Journal of Homotopy and Related Structures (JHRS) is a fully refereed international journal dealing with homotopy and related structures of mathematical and physical sciences. Journal of Homotopy and Related Structures is intended to publish papers on Homotopy in the broad sense and its related areas like Homological and homotopical algebra, K-theory, topology of manifolds, geometric and categorical structures, homology theories, topological groups and algebras, stable homotopy theory, group actions, algebraic varieties, category theory, cobordism theory, controlled topology, noncommutative geometry, motivic cohomology, differential topology, algebraic geometry.